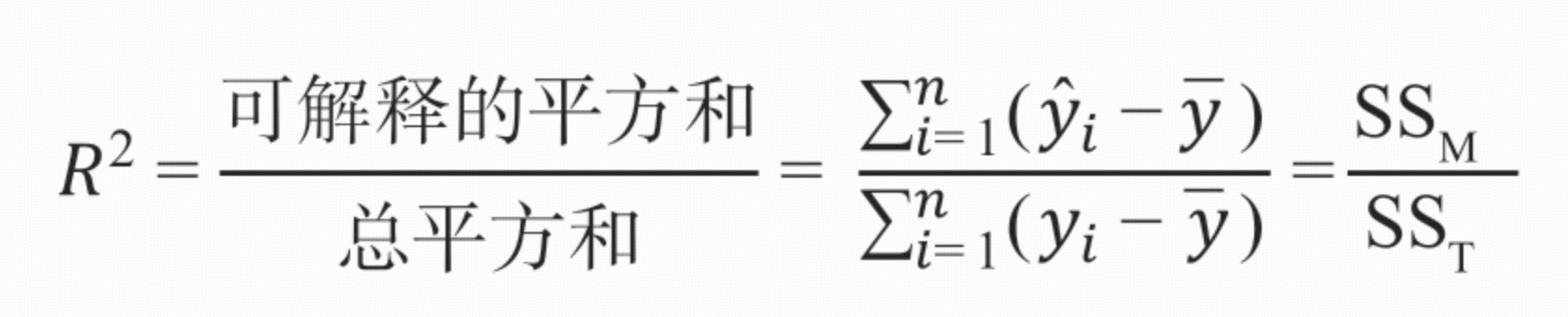线性回归模型评价指标 R²：

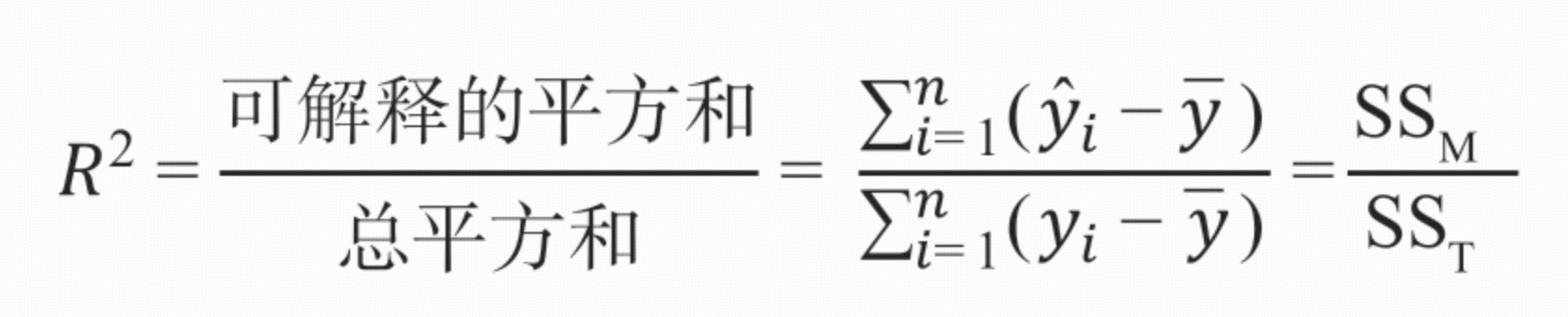
可解释的总平方和为 y的预测值-y的均值 的 平方和

总平方和为 y 值的总离差平方和（y-y的均值 的 平方和）：描述数据波动的总量

• 总离差平方和：是各观测值$y_i$与均值$\bar{y}$离差的平方和，即$SST={\sum }_{i=1}^n(y_i-\bar{y}{)}^2$，它反映了因变量$y$取值的总波动程度。例如，在上述例子中，$SST=40$，体现了$y$值相对于均值$6$的总体波动大小。

• 方差：方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量，是每个样本值与全体样本值的平均数之差的平方值的平均数，其计算公式为$s^2=\frac{1}{n}{\sum }_{i=1}^n(y_i-\bar{y}{)}^2$。可以看出，方差是总离差平方和除以样本数量$n$得到的。比如上述例子中，数据的方差$s^2=\frac{40}{5}=8$。

• 总离差平方和是方差的分子部分，将总离差平方和除以样本数量就得到了方差。二者都用于衡量数据的离散程度，但总离差平方和更侧重于描述数据波动的总量，方差则是从平均意义上衡量数据的离散程度。

可解释的平方和（Sum of Squares due to Regression，SSR），也叫回归平方和，是在回归分析中用于衡量回归模型对因变量变化解释程度的一个指标。具体如下：

• 定义：它表示因变量的预测值\(\hat{y}_i\)与均值\(\bar{y}\)之差的平方和，计算公式为\(SSR=\sum_{i = 1}^{n}(\hat{y}_i-\bar{y})^2\)。其反映了自变量x的变化通过回归直线对因变量y的线性影响所引起的波动程度，也就是回归模型能够解释的那部分因变量的变异。

• 作用：SSR 的值越大，说明回归模型对数据的拟合效果越好，即自变量对因变量的解释能力越强。例如，在一元线性回归分析中，如果SSR接近总离差平方和SST，则说明大部分的因变量变异可以由回归模型来解释，\(R^2=\frac{SSR}{SST}\)就会接近1，表示回归直线与观测数据点拟合得很好。反之，如果SSR较小，说明回归模型能够解释的因变量变异较少，拟合效果可能不理想。

比如，在前面给出的示例中，计算得到\(SSR = 40\)，这意味着基于自变量x建立的回归模型能够解释因变量y的40个单位的变异，由于\(SST = 40\)，所以\(R^2 = 1\)，说明该回归模型完全解释了因变量的变化，拟合效果非常好。

线性于参数：

“线性回归中的‘线性于参数’” 可以通俗地理解为回归模型中参数与因变量之间是线性关系，以下从模型形式、函数图像、实际意义等方面详细解释：

• 模型形式：在线性回归模型中，因变量是由自变量和参数通过线性组合构成的。以一元线性回归为例，其模型表达式为\(y = \beta_0+\beta_1x+\epsilon\)，其中y是因变量，x是自变量，\(\beta_0\)和\(\beta_1\)是参数，\(\epsilon\)是误差项。这里\(\beta_0\)和\(\beta_1\)都是以一次方的形式出现，没有与其他参数相乘、相除、平方、开方等非线性运算，它们对y的影响是线性的。如果是多元线性回归\(y=\beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_nx_n+\epsilon\)，同样每个参数\(\beta_i\)也都是线性地影响y。

• 函数图像：从几何角度看，线性于参数的回归模型在图像上表现为直线（一元线性回归）或超平面（多元线性回归）。比如在一元线性回归中，\(\beta_0\)是直线在y轴上的截距，\(\beta_1\)是直线的斜率，决定了直线的倾斜程度。由于参数是线性的，所以随着自变量x的变化，因变量y沿着这条直线线性变化。

• 实际意义：在实际问题中，“线性于参数” 意味着当自变量发生变化时，因变量的变化是由各个参数以线性的方式共同作用的结果。例如，在研究身高x与体重y的关系时，若建立的一元线性回归模型为\(y = \beta_0+\beta_1x+\epsilon\)，\(\beta_0\)表示当身高为0时体重的基础值（实际意义可能不大），\(\beta_1\)表示身高每增加一个单位，体重平均增加的量。这里\(\beta_0\)和\(\beta_1\)对体重y的影响是相互独立且线性的，即体重的变化是由\(\beta_0\)和\(\beta_1\)与身高x的线性组合决定的。