从原理上讲，“对数几率回归”这个名称更准确地反映了逻辑回归模型的本质。因为在这个模型中，关键的步骤是先对事件发生的几率取对数，得到对数几率（log - odds），然后将对数几率建模为自变量的线性组合最后再通过逻辑函数（Sigmoid函数）将对数几率转换回概率。

一、逻辑回归的正确理解

1、名称来源的合理性

    从原理上讲，“对数几率回归”这个名称更准确地反映了模型的本质。因为在这个模型中，关键的步骤是先对事件发生的几率(p/1−p)取对数，得到对数几率，然后将对数几率建模为自变量的线性组合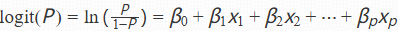，最后再通过逻辑函数（Sigmoid函数）将对数几率转换回概率，整个过程对数几率的构建和处理是核心，所以“对数几率回归”这个名字更能体现其内在的数学原理。

2、历史和习惯因素导致“逻辑回归”名称的使用

    历史沿用：在统计学和机器学习的发展过程中，由于早期的习惯和某些历史文献的引导，“逻辑回归”这个名称被广泛使用。最初可能是因为重点被放在了逻辑函数（Sigmoid函数）的使用上，它将线性组合的结果（对数几率）转换为概率，这个转换过程比较直观和容易理解，所以人们就简单地称之为“逻辑回归”。

    应用场景的关注重点：在实际应用中，很多使用者更关注模型的输入（自变量）和输出（概率预测），而对于中间的对数几率建模过程可能没有深入探究。他们主要是利用这个模型来进行分类，比如判断一个样本属于某一类别的概率是高于还是低于0.5，进而做出分类决策。这种在应用层面关注逻辑分类的特点，也使得“逻辑回归”这个名称更容易被接受和使用。

3、两种名称的并存与理解的重要性

    虽然“逻辑回归”这个名称使用更为广泛，但理解“对数几率回归”这个名称有助于深入掌握模型的工作原理。无论是从理论研究还是模型改进的角度来看，清楚地认识到模型是基于对数几率进行回归分析的，对于正确使用和拓展这个模型都非常重要。在学术交流和深入学习的过程中，同时理解这两个名称及其背后的含义，可以更好地与不同背景的人沟通，也有助于更准确地把握模型的本质和应用范围。

二、背景

1、线性模型的发展及需求产生

    在统计学的早期发展阶段，线性模型是一种被广泛理解和应用的工具。线性回归在分析变量之间的关系方面已经取得了显著的成果，它能够有效地处理连续型因变量和自变量之间的关系，并且有着相对成熟的理论基础和计算方法。例如，在经济学领域，通过线性回归可以研究收入与消费之间的线性关系；在物理学中，线性模型可以用于描述一些物理量之间的关系。

    这就产生了一种强烈的需求，即找到一种方法将概率问题转化为可以用线性模型处理的形式，从而能够利用线性模型的优势来解决分类问题。

2、逻辑回归的诞生

    为了克服上述困难，统计学家引入了逻辑函数和对数几率（log - odds）的概念，最初的灵感可能来源于对概率和线性关系之间的探索，通过对几率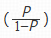取对数得到对数几率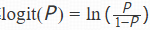，发现对数几率的取值范围是从负无穷到正无穷，这就与线性模型的输出范围相匹配。

    然后，将对数几率表示为自变量的线性组合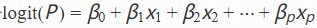，就可以利用线性模型的理论和方法来估计参数β0,β1,⋯ ,βp。最后，再通过逻辑函数将对数几率转换回概率P=σ(β0+β1x1+β2x2+⋯+βpxp)，从而实现了将概率问题转化为可以用线性模型处理的问题，诞生了对数几率回归这一强大的分类工具。

三、萌芽

1、起源于分类问题

    逻辑回归LogisticRegressionLogisticRegression起源于对分类问题的研究需求。在许多实际场景中，需要根据一些特征变量来预测一个事件属于某一类别的概率，例如根据患者的症状、检查结果等特征来判断是否患有某种疾病（二分类问题），或者根据用户的行为、属性等特征来预测用户是否会购买某产品（二分类问题），以及文本分类、图像识别中的类别判断等多分类问题。传统的线性回归模型不适用于分类问题，因为其预测值是连续的，可能超出分类标签的范围，逻辑回归应运而生。

2、理论基础

    它的理论基础与概率和统计学中的一些概念密切相关。逻辑回归模型的构建借鉴了线性回归的思想，并结合了对数几率的概念，将线性函数的结果转换为概率值，从而能够用于分类任务。

四、几率和对数几率的概念

1、几率

    几率 Odds：在生活中，我们可把几率理解为事件发生的可能性和不发生的可能性的比值。还是以购买产品为例，假设购买产品的概率是P，那么不购买的概率就是1−P，这时几率Odds=P/(1−P)。比如，购买产品的概率是0.6，不购买的概率就是0.4，那么几率就是 0.6/0.4=1.5。

2、对数几率

    对数几率Log−Odds：对几率取对数，得到的就是对数几率。在对数几率回归中，我们是对这个对数几率进行建模。为什么要这样做呢？因为直接对概率建模比较复杂，而对数几率的范围是从负无穷到正无穷，这样就可以用线性函数来拟合了。就好像把概率这个“调皮的小家伙”通过对数几率这个“桥梁”，让它能够和线性函数配合起来。

    当我们有了新的数据（一个人的年龄、收入、性别等特征），先通过线性组合（把这些特征乘以对应的系数然后相加）得到一个数值，这个数值就是对数几率。然后通过一个特殊的函数把对数几率再转换回概率。σ(z)的样子像一个“S”，它可以把从负无穷到正无穷的数值转换为0到1之间的概率。例如，如果计算出的概率大于0.5，我们就可以预测这个人会购买产品；如果小于0.5，就预测这个人不会购买产品。这样就完成了分类预测的过程。

五、对数几率的计算

1、对数几率的计算公式

    对数几率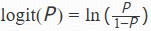：，其中P是事件发生的概率，ln⁡表示自然对数。

2、取值范围的边界情况示例

3、中间值示例

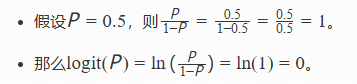
    可以看到当概率P=0.5时，对数几率为0。这也说明对数几率在概率为0.5时处于中间位置，其取值范围以0为中心向两边延伸到负无穷和正无穷，符合概率与对数几率之间的转换关系。

六、逻辑函数（Sigmoid）转换

1、逻辑函数（Sigmoid函数）的表达式

    逻辑函数的表达式为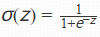，在对数几率回归中，z就是对数几率logit(P)=β0+β1x1+β2x2+⋯+βpxp，这里x1,x2,⋯ ,xp是自变量，β0,β1,⋯ ,βp是模型的参数。

2、转换过程示例

3、从函数图像角度理解

    逻辑函数σ(z)的图像是一个“S”形曲线。当z趋于负无穷时，e^−z趋于正无穷，1+e^−z也趋于正无穷，此时σ(z)趋于0；当z趋于正无穷时，e^−z趋于0，σ(z)趋于1。这正好符合概率的取值范围在0到1之间的要求，使得对数几率能够通过这个函数合理地转换回概率，用于表示事件发生的可能性大小。