时间序列数据是对某个个体在多个时间点上收集的数据。本章的主要内容有时间序列简介、趋势分解法时间序列分析、ARIMA时间序列分析等。

一、认识时间序列

    在实际分析工作中，会遇到很多与时间序列有关的数据。比如，某电商平台每个月的全国销售额、某网站一个月内的日访问量等。时间序列数据是按时间顺序排列、随时间变化且相互关联的数据序列。

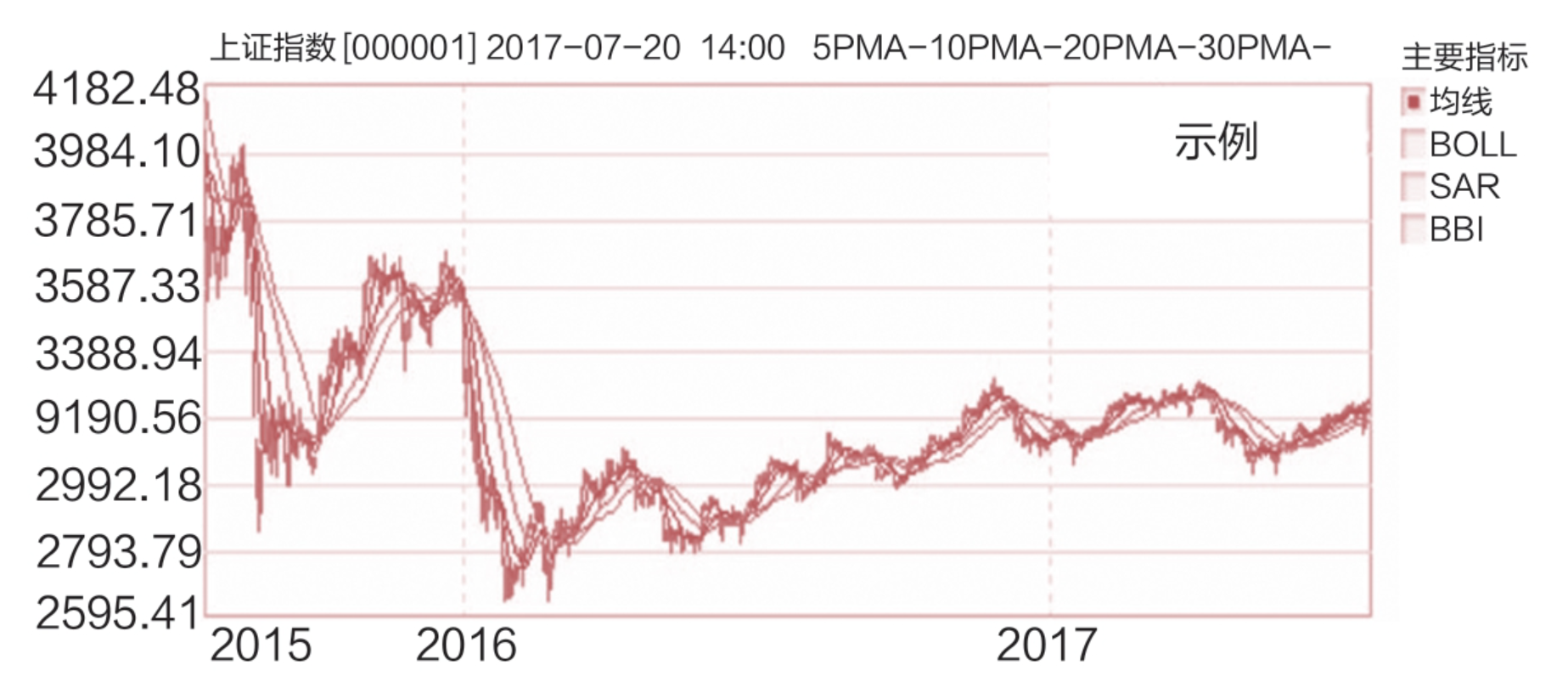
    根据所研究的依据不同，时间序列有不同的分类。按研究对象可以分为一元时间序列和多元时间序列，按时间属性可分为离散时间序列和连续时间序列，按序列的特性可以分为平稳时间序列和非平稳时间序列。

    初级常用的时间序列数据的分析方法有两类：一类为效应分解法，即把时间序列分解为趋势效应和周期性效应，并分别使用曲线拟合；另一类为ARIMA方法，该方法可以针对数据产生的机理构建动态模型，实际上是根据数据扰动项之间的相关性结构构建预测模型的。

二、效应分解法

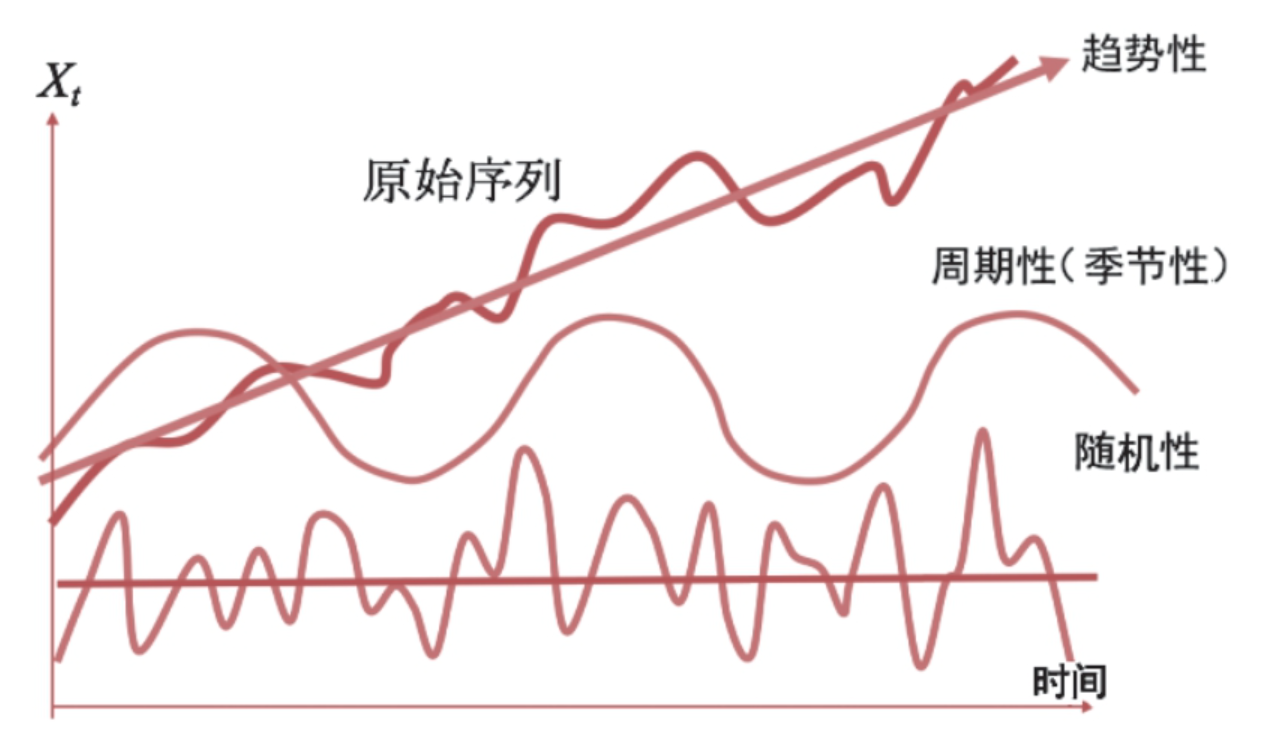
    气温、自然景点游客流量等时间序列数据可以分解为趋势性、周期性/季节性、随机性3个主要组成部分。其中，前两个部分属于时间序列中的稳定部分，可以用于预测未来。

1、时间序列的效应分解

    (1)趋势性：是指序列朝着一定的方向持续上升或下降，或者停留在某个水平上的倾向。它反映了客观事物的主要变化趋势，比如随着企业近段时间拓展业务，销售额稳步上升的趋势。

    (2)周期性\季节性变动：周期性通常是指经济周期，由非季节因素引起的波形相似的波动，比如GDP增长率随经济周期的变化而变化。但是周期性变动稳定性不强，在实际操作中很难考虑周期性变动，主要考虑的是季节性变动。季节性变动是指季度、月度、周度、日度的周期变化，比如啤酒的销量在春季、夏季较高而在秋季、冬季较低，郊区的加油站人流量在周末多而周中少，交通流量在上班高峰多而在其他时间少。

    (3)随机性：随机变动是指由随机因素导致的时间序列的小幅度波动。

2、时间序列3种效应的组合方式

    (1)加法模型，即三种效应是累加的。

    x_t=T_t+S_t+I_t

    其中，T_t代表趋势效应，S_t代表季节效应，I_t代表随机效应。

    (2)乘积模型，即三种效应是累计的。

    x_t=T_t×S_t×I_t

    累计预测出的时间序列数据会叠加趋势，从而使得周期振荡的幅度随着趋势的变化而变化。

三、平稳时间序列分析ARMA模型

1、平稳时间序列

    在统计学中，平稳时间序列分为严平稳时间序列与宽平稳时间序列两种。 

    如果在一个时间序列中，各期数据的联合概率分布与时间t无关，则称该序列为严平稳时间序列。但是在通常情况下，时间序列数据的概率分布很难获取与计算，实际讨论的平稳时间序列是指在任意时间下，序列的均值、方差存在且为常数，自协方差函数和自相关系数只与时间间隔k有关，而与时间t无关。

    只有平稳时间序列才可以进行统计分析，因为平稳性保证了时间序列数据都出自同一个分布，这样才可以计算均值、方差、延迟k期的协方差、延迟k期的相关系数等。

    一个独立同标准正态分布的随机序列就是平稳序列，如图：

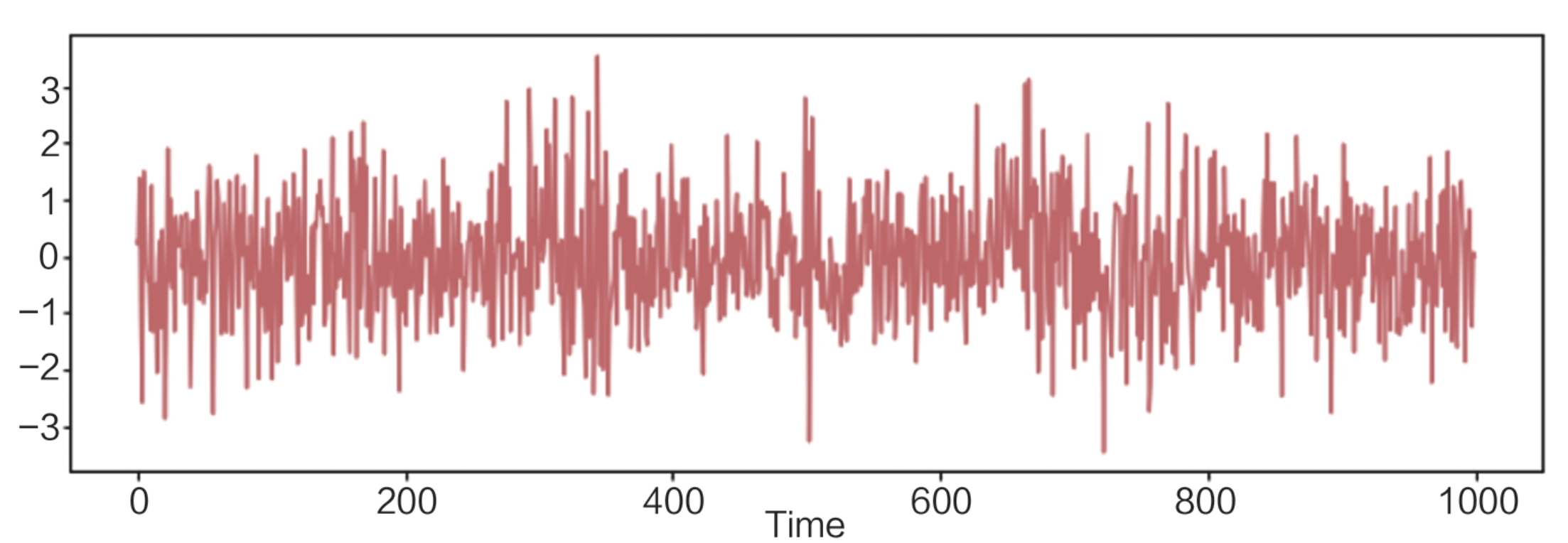
    当然，若一个平稳时间序列的序列值之间没有相关性，那么就意味着这种数据前后没有规律，也就无法挖掘有效的信息，这种序列被称为纯随机序列。在纯随机序列中，有一种序列被称为白噪声序列，这种序列随机且各期的方差一致。

    平稳时间序列分析在于充分挖掘时间序列之间的关系，当时间序列中的关系被提取出来后，剩下的序列就应该是一个白噪声序列。

平稳时间序列模型主要有以下3种：

(1)自回归模型(Auto Regression Model)，即AR模型。

(2)移动平均模型(Moving Average Model)，即MA模型。

(3)自回归移动平均模型(Auto Regression Moving AverageModel)，即ARMA模型。

    用于判断ARMA模型的自相关和偏自相关函数如下：

    (1)自相关函数(Autocorrelation Function, ACF)：描述任意两个时间间隔为k的时间序列的相关系数。

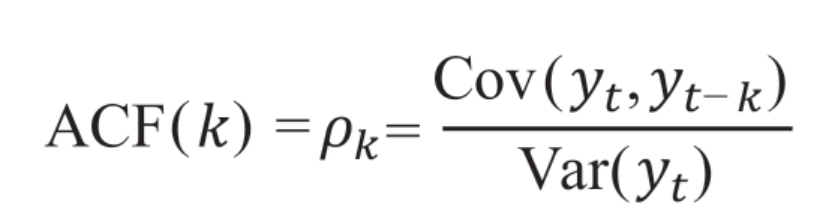
    (2)偏自相关函数(Partial Autocorrelation Function,PACF)：描述时间序列任意两个时间间隔k的时刻，去除1至k-1这个时间段中的其他数据的相关系数，在统计学中被称为偏相关系数。

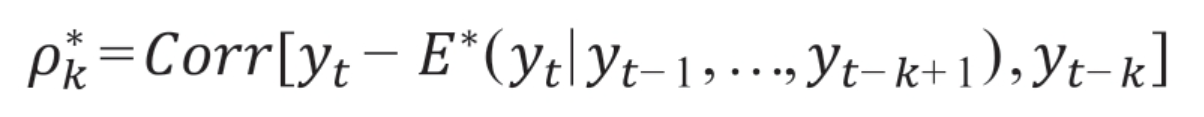
2、ARMA模型

1）AR模型

    AR模型又被称为自回归模型，认为时间序列当期观测值与前p期有线性关系，而与前p+1期无线性关系。

    假设时间序列Xt仅与Xt-1，Xt-2，…，Xt-p有线性关系，而在Xt-1，Xt-2，…，Xt-1已知条件下，Xt与Xt-1(j=p+1,p+2…)无关，εt是一个独立于Xt的白噪声序列：

    可见，在AR(p)系统中，Xt具有p阶动态性。AR(p)模型通过把Xt中的依赖Xt-1，Xt-2，…，Xt-p的部分消除后，使得具有p阶动态性的时间序列Xt转换为独立的序列。因此，拟合AR(p)模型的过程也是使相关序列独立化的过程。

    以AR(1)模型为例，其中(1)代表滞后1期。

AR(p)模型有以下重要性质：

(1)某期观测值Xt的期望与系数序列α有关，方差有界。

(2)自相关系数(ACF)拖尾，且值呈现指数衰减（时间越近的往期观测对当期观测的影响越大）。

(3)偏自相关系数(PACF)p阶截尾。

其中，ACF与PACF的性质可以用于识别该平稳时间序列是适合滞后多少期的AR模型。

2）MA模型

    MA模型认为如果一个系统在t时刻的响应Xt，与其以前时刻t-1，t-2，…的响应Xt-1，Xt-2，…无关，而与其以前时刻t-1，t-2，…，t-q进入系统的扰动项εt-1，εt-2，…，εt-q存在着一定的相关关系，那么这类系统为MA(q)模型。

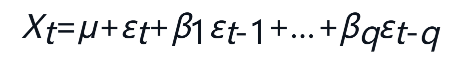
    其中，εt是白噪声过程。

MA(q)模型有以下重要性质：

(1)t期系统扰动项εt的期望为常数，方差为常数。

(2)自相关系数(ACF)q阶截尾。

(3)偏自相关系数(PACF)拖尾。

其中，ACF与PACF的性质可以用于识别该平稳时间序列是适合滞后多少期的MA模型。

3）ARMA模型

    ARMA模型即自回归移动平均模型，该模型结合了AR模型与MA模型的特点，认为序列受前期观测数据与系统扰动的共同影响。

    具体来说，一个系统，如果它在时刻t的响应Xt不仅与其以前时刻的自身值有关，而且还与其以前时刻进入系统的扰动项存在一定的依存关系，那么这个系统就是自回归移动平均模型。

    ARMA(p, q)模型如下：

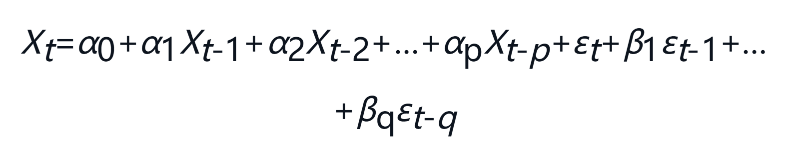
    其中，εt是白噪声过程。

    对于平稳时间序列来说，AR(p)模型、MA(q)模型、ARMA(p, q)模型都属于ARMA(p, q)模型的特例。

ARMA(p, q)模型的性质有以下几点：

(1)Xt的期望与系数序列α有关，方差有界。

(2)自相关系数(ACF)拖尾。

(3)偏相关系数(PACF)拖尾。

4）ARMA模型的定阶与识别

    自相关系数(ACF)与偏自相关系数(PACF)可以用于判断平稳时间序列数据适合哪一种模型和阶数。

    (1)下面是一个AR(1)模型，时序图如图

    Y_t=0.6Y_t-1+ε_t

    ε_t～N(0, σ²)

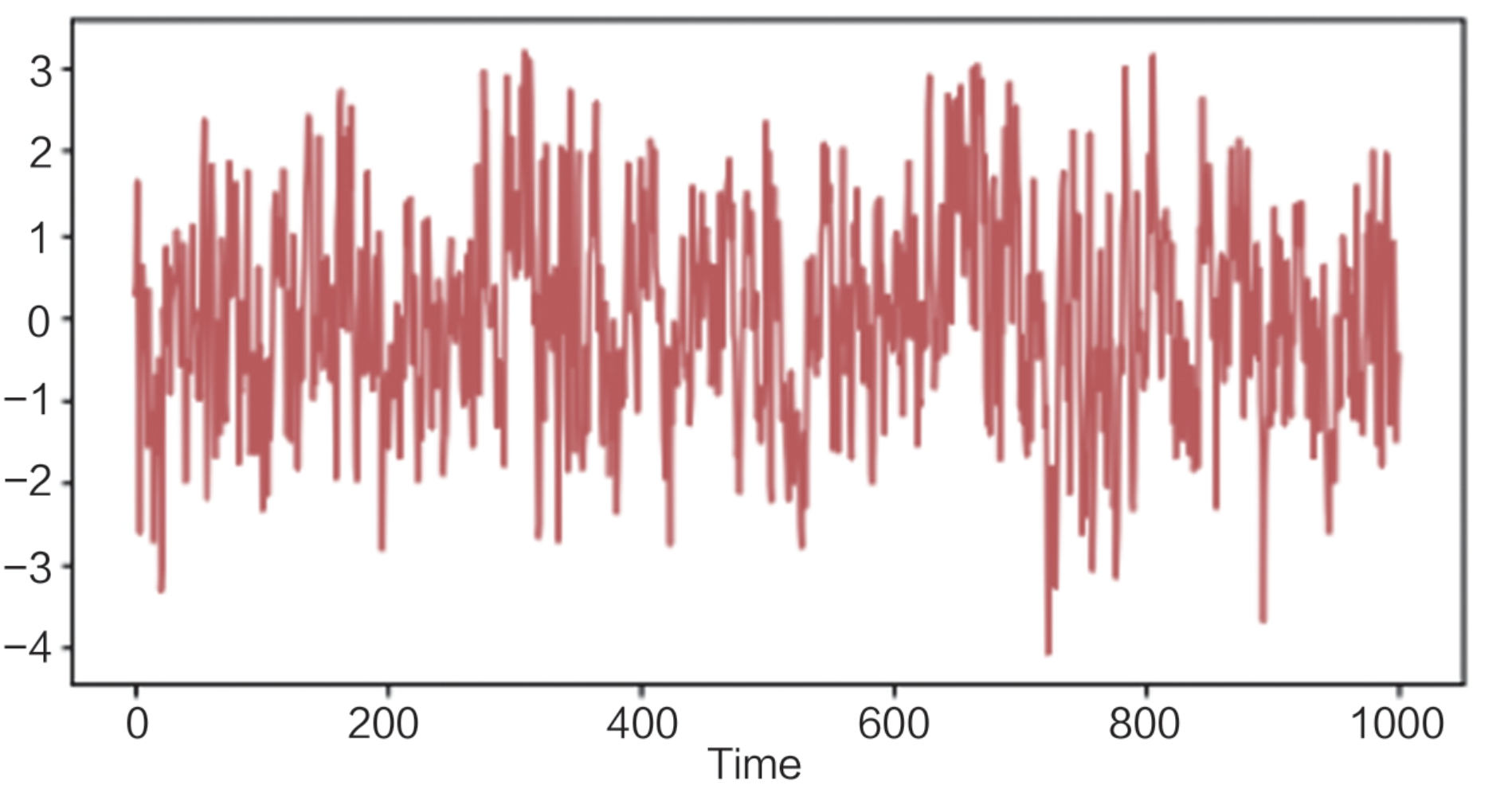
    AR模型ACF拖尾，PACF为1阶截尾，自相关图和偏自相关图分别如图

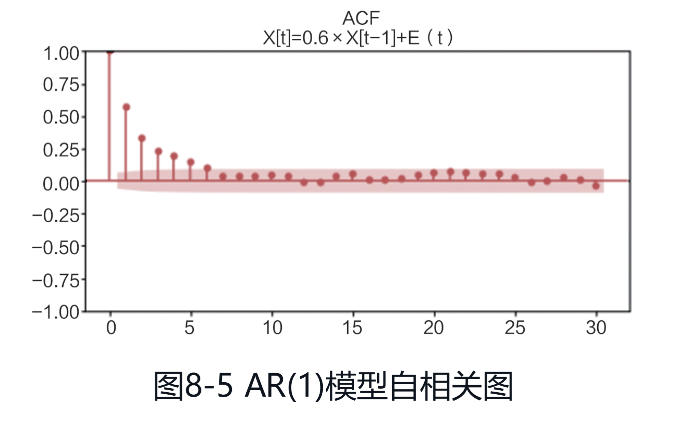
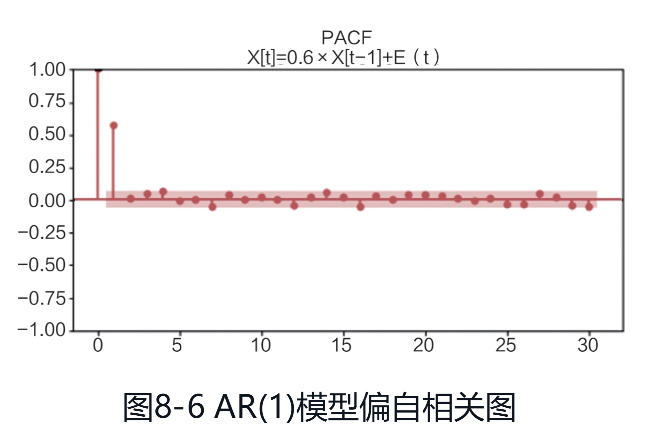
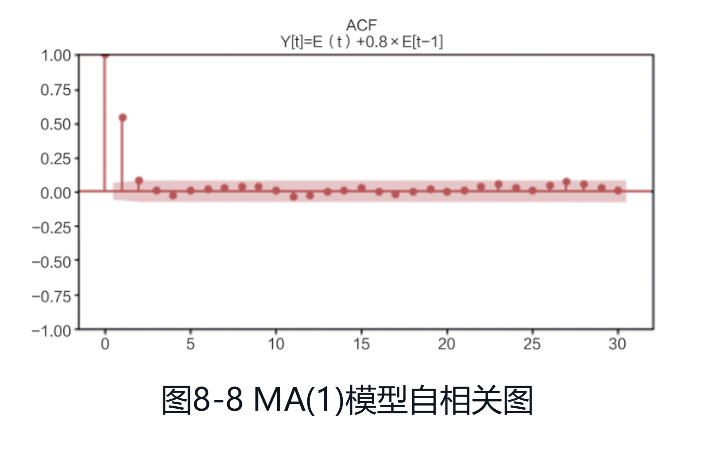
    (2)下面是一个MA(1)模型，时序图如图：

    Y_t=ε_t+0.8ε_t-1

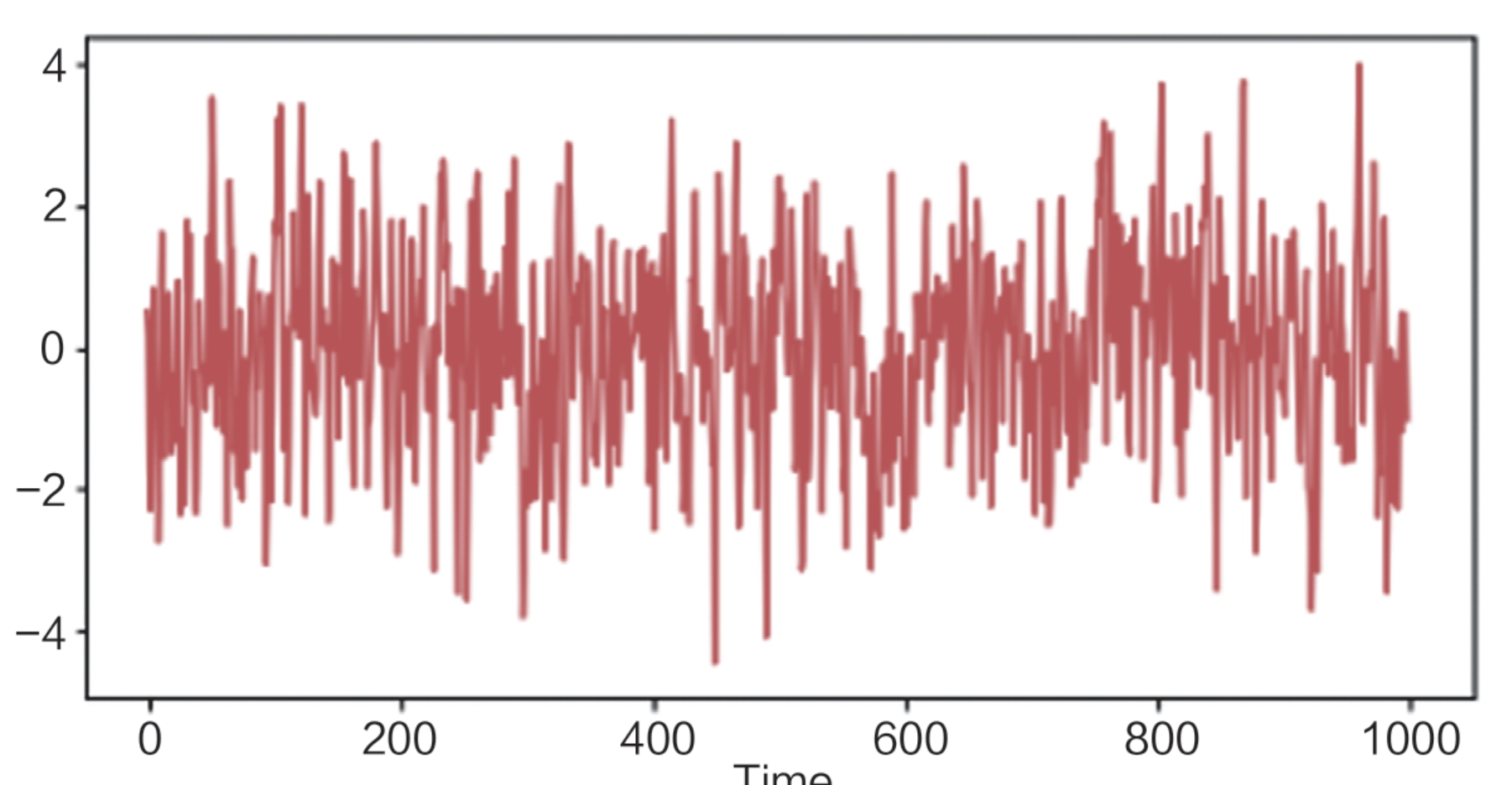
    MA模型RACF为1阶截尾，PACF拖尾，自相关图和偏自相关图分别如图：

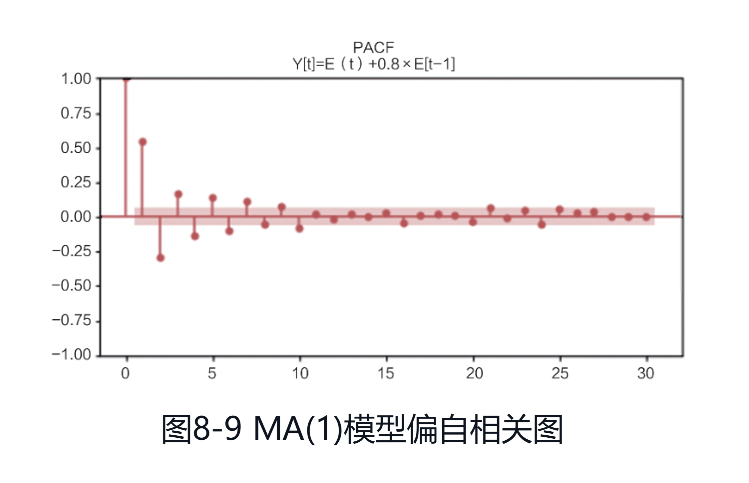
    (3)下面是一个ARMA(1, 1)模型，时序图如图：

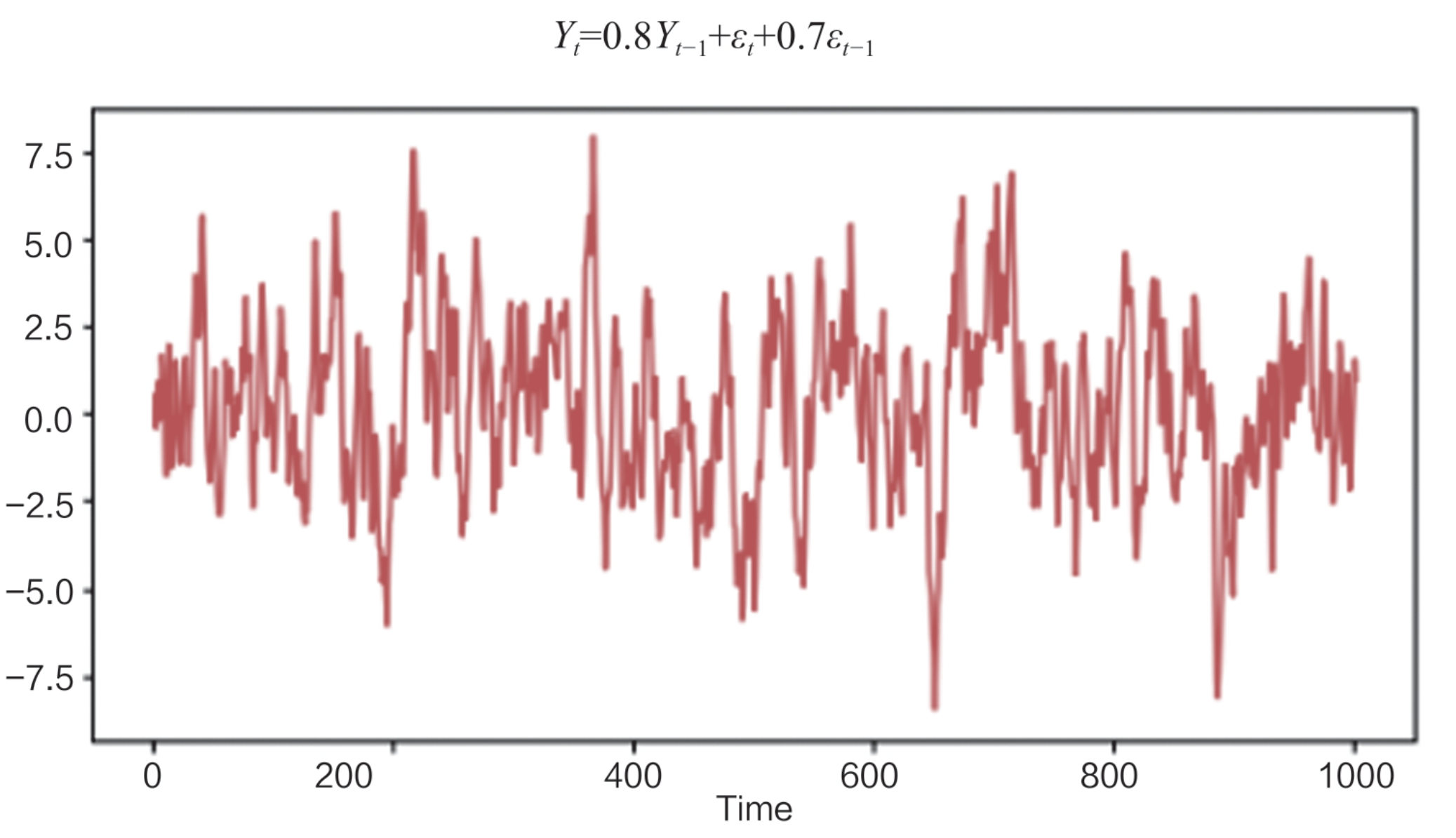
    ARMA模型的ACF与PACF都是拖尾的情形，自相关图和偏自相关图分别如图：

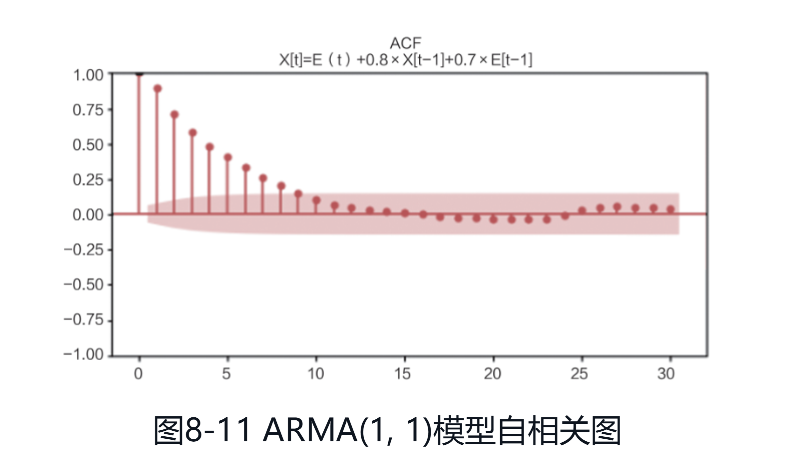
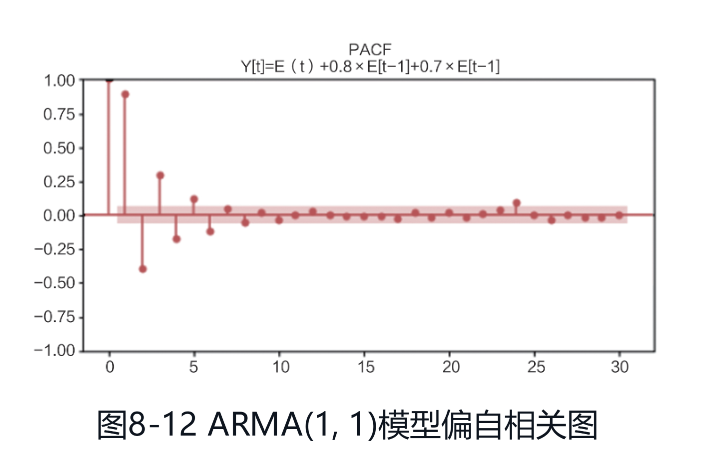
    综上所述，ACF和PACF定阶的准则如下：

    一般要求样本长度大于50才会有一定的精确程度。在使用ACF与PACF对ARMA模型进行定阶时，只能精确到定阶MA模型与AR模型的阶数，而无法确定ARMA模型的阶数，而且由于估计误差的存在，实际中有时甚至很难判断AR模型与MA模型的截尾期数。

    在实际操作中识别ARMA模型的阶数时，通常使用AIC或BIC准则进行识别，两个统计量都是越小越好，AIC或BIC准则特别适合用于ARMA模型的定阶，当然也适用于AR模型和MA模型。

3、在Python中进行AR建模

四、非平稳时间序列分析ARIMA模型

    经过差分处理，将非平稳时间序列转换为平稳时间序列，再用ARIMA建模

1、差分与ARIMA模型

1）差分运算

    差分运算是一种非常简便、有效的确定性信息提取方法，而Cramer分解定理在理论上保证了适当阶数的差分一定可以充分提取确定性信息。

    差分运算的实质是使用自回归的方式提取确定性信息，1阶差分即当期观测减前一期的观测构成差分项，其数学表达式为：

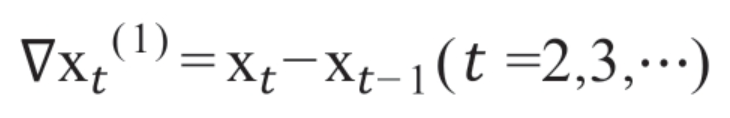
    2阶差分是在1阶差分的基础上，对1阶差分的结果再进行差分，其数学表达式为：

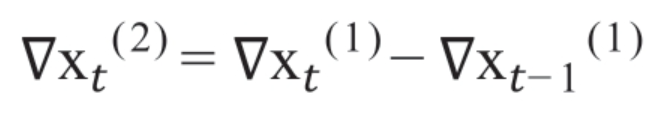
    以此类推，d阶差分是在d-1阶差分的基础上，对d-1阶差分的结果再进行差分，其数学表达式为：

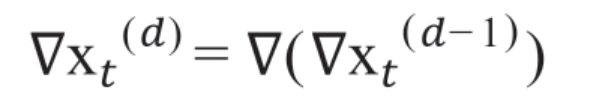
    适度的差分能够有效地将非平稳时间序列转换为平稳时间序列。如图所示的原始数据时序图有着明显的趋势性。

    经过1阶差分处理和2阶差分处理的结果分别如图：

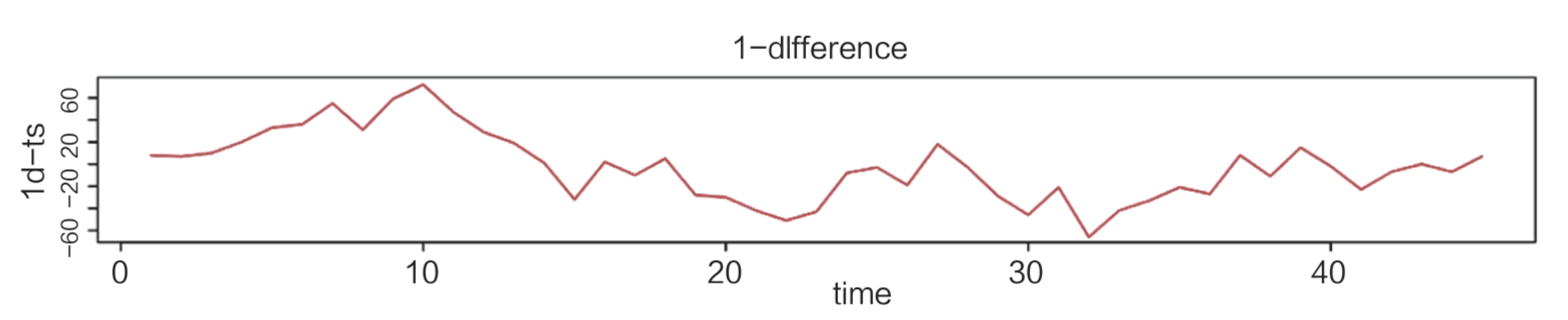
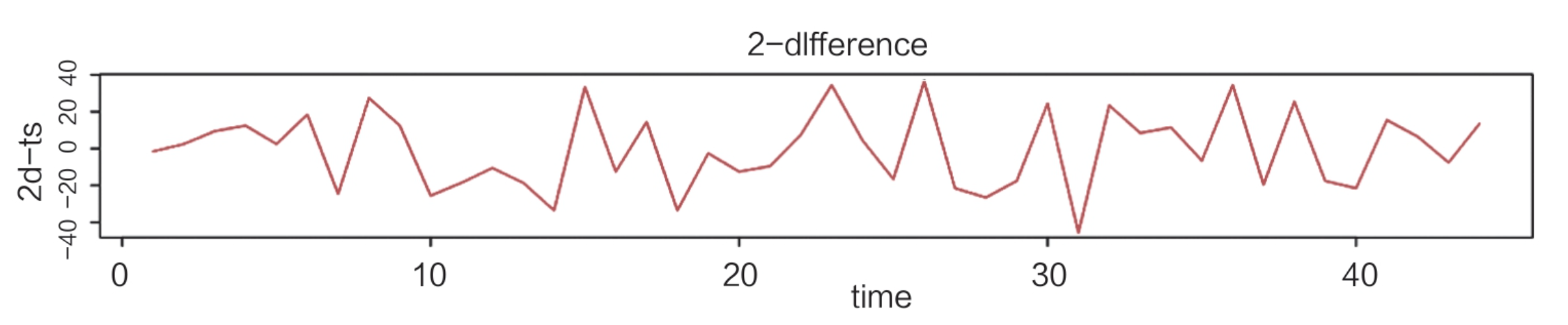
    对于有季节性的数据，可以采用一定周期的差分运算（季节差分）提取季节信息，季节差分数学表达式如下，s表示周期：

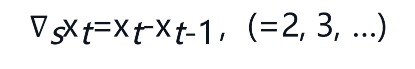
    在季节差分的基础上再进行一般的差分就可以同时提取季节性与周期性，s期d阶的差分表达式如下：

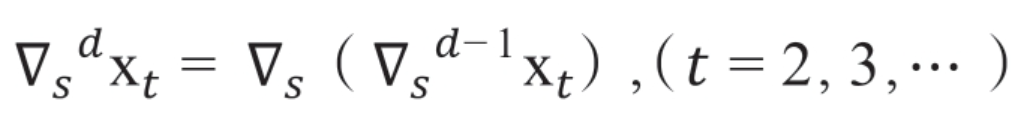
    如图是一个带有季节性的数据，周期为12期：

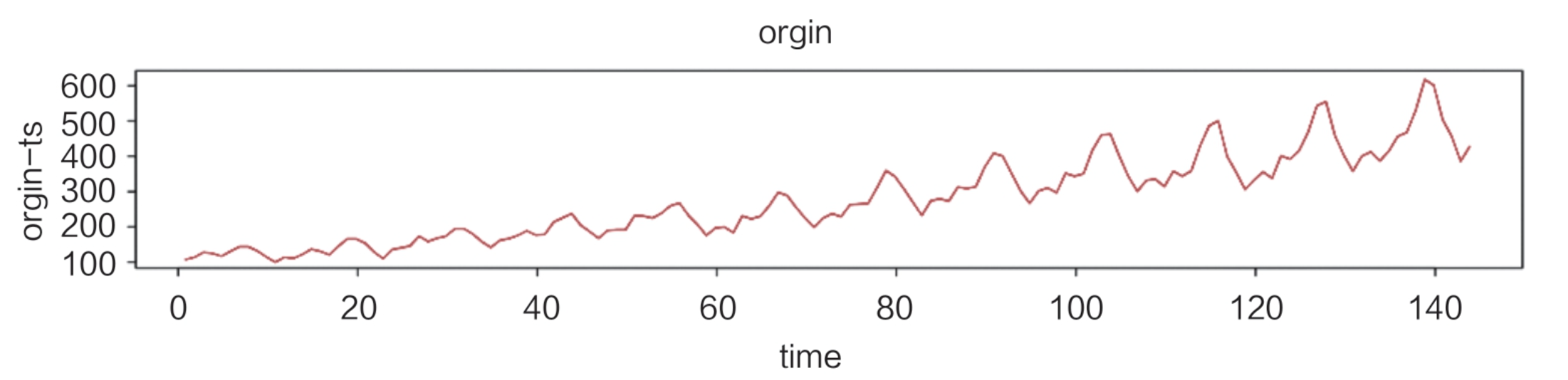
    一阶差分处理后：

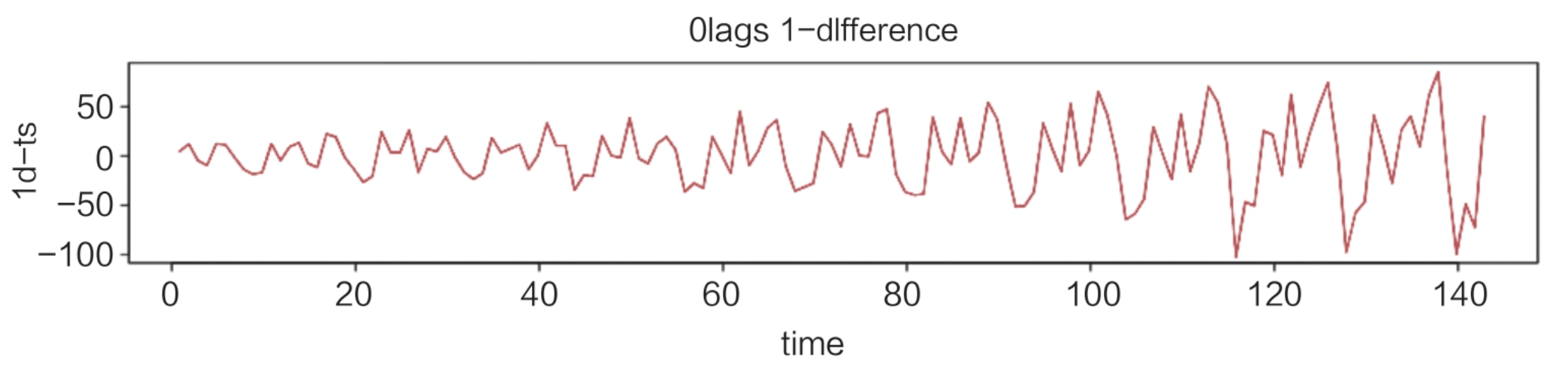
    一阶差分与12阶季节差分处理后：

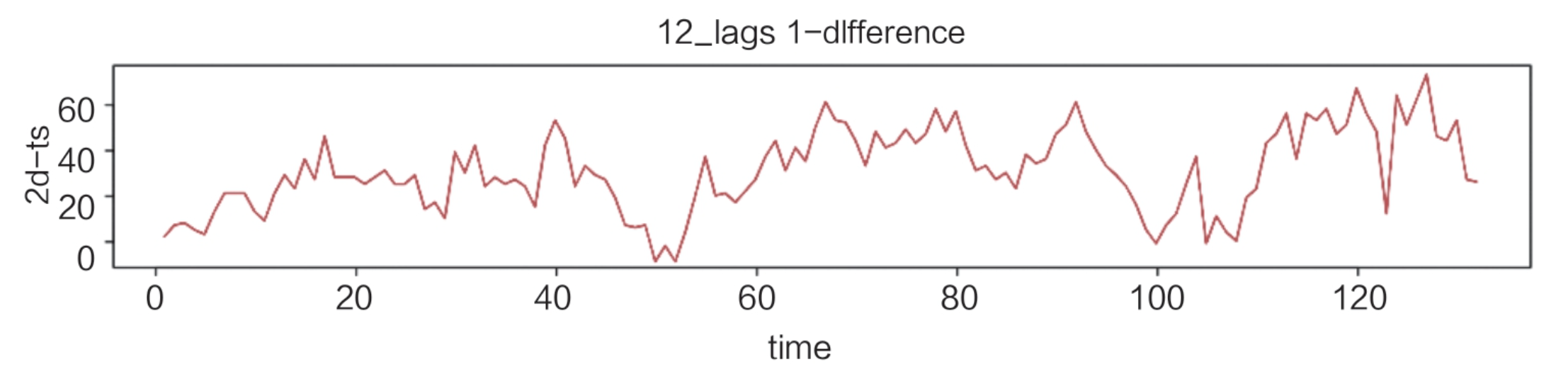
    需要注意的是，差分应适度，否则会造成信息的浪费，一般在实际操作中，使用2阶差分足够提取序列的不稳定信息。

2）ARIMA模型的建模步骤

    ARIMA模型适用于非平稳时间序列数据，其中的I表示差分的阶数，使用适当的差分处理将原始序列转换为平稳序列后，再进行ARIMA建模。

    ARIMA建模步骤与ARMA建模步骤类似，分为以下5步：

(1)平稳化：通过差分的手段，对非平稳时间序列数据进行平稳化处理。

(2)定阶：确定ARIMA模型的阶数p、q。

(3)估计：估计未知参数。

(4)检验：检验残差是否是白噪声序列。

(5)预测：利用模型预测。

2、在Python中进行ARIMA建模

五、ARIMA建模方法总结

    在商业时间序列预测方面，可遵循以下建模流程：

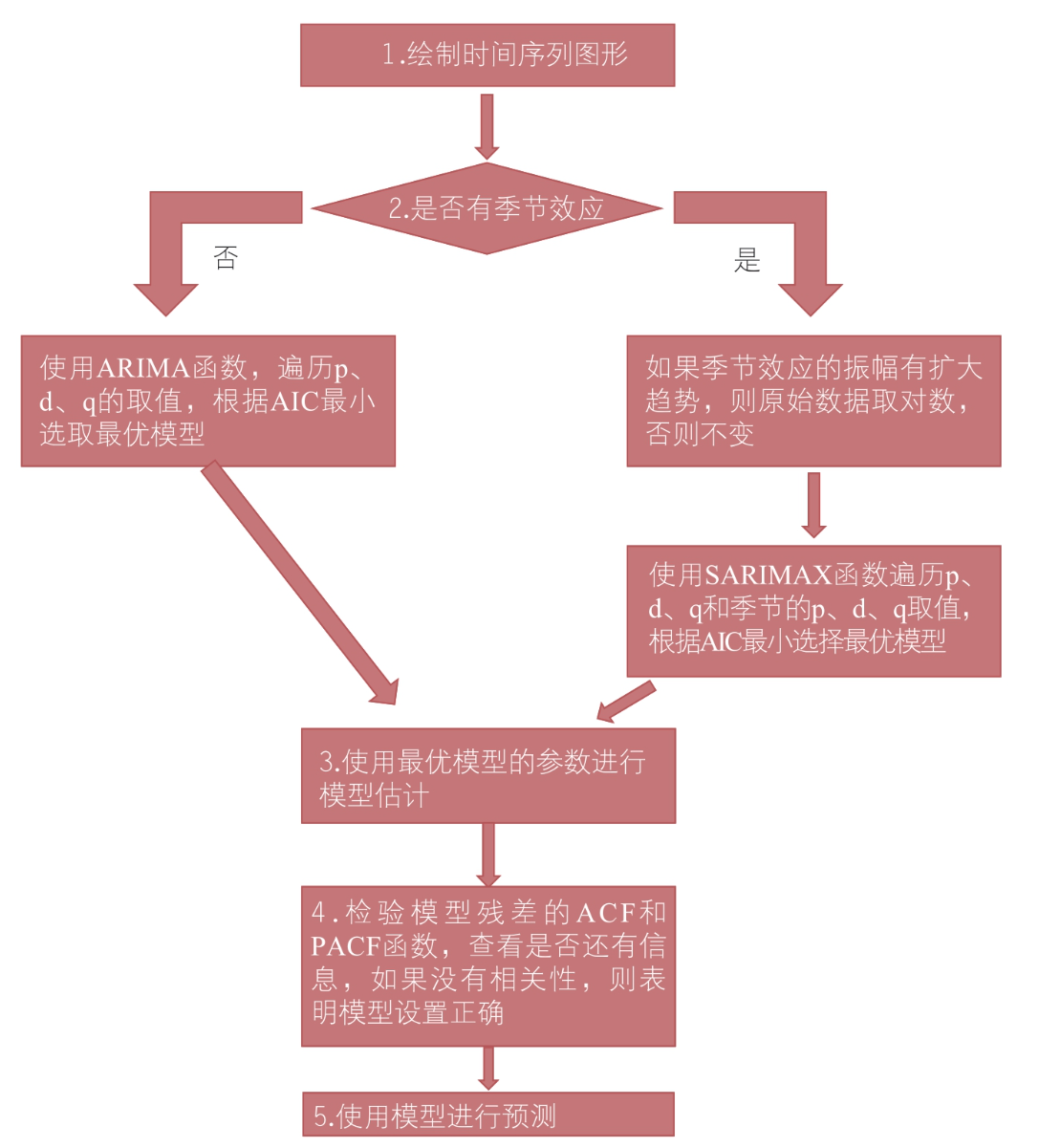
    步骤1：该步骤是必需的，如果不看时间序列图形，就不能确定是否有季节效应。可能有人认为，既然SARIMAX函数的功能可以涵盖ARIMA函数的动能，就可以统一使用SARIMAX函数遍历所有参数，得到最优模型。但是这样做是不可取的，因为SARIMAX函数的参数过多，模型的估计结果不稳定。如果数据没有季节效应，则尽量选择ARIMA函数进行估计。

    步骤2：参数的取值是0、1、2，很少有参数超过2的情况，即使真的超过2，第3阶的信息也很少，可以忽略。实在有问题，还可以在步骤4中通过查看残差的情况判断是否扩大搜索空间。选取最优模型可以依据AIC或BIC统计量，依据AIC统计量选取的模型较大，即模型参数较多；依据BIC统计量选取的模型较小，即模型参数较少。不过绝大部分情况下两个统计量得到的模型是一样的。

    步骤3：对步骤3得到的最优模型进行重新估计。模型估计好后，可以查看模型的参数。本步骤并没有进行时间序列的平稳性检验，有两个考虑：①平稳性检验的方法众多，远不只本章介绍的一种检验方法，也比较复杂，statsmodels中提供的adfuller函数其实聊胜于无，用处并不大；②目前统计学界提供的平稳性检验方法的势(power)都不高，也就是说，检验结果没有很大用处。实际上，相关系数为0.9以上的AR(1)和ARIMA(0, 1, 0)是不能通过平稳性检验区分开的。因此索性不做平稳性检验，仅依靠AIC或BIC统计量判断最优模型即可。

    步骤4：该步骤用于确认模型的正确性。如果残差序列的前几阶（比如5阶）自相关性、偏自相关性不显著，则说明已经是最优模型。统计学参考书中会使用DW统计量（杜宾-沃森检验）、Q-Q检验、Q检验，其实和查看自相关函数区别不大。

    步骤5：在本步骤中，如果之前的数据取了自然对数，则在使用模型预测后，要对数据取自然指数。