一、用户细分与聚类

    20世纪90年代之前，主要使用用户基本信息进行细分，之后代表性的企业开始将人口统计学和心理学知识融入用户分群，为不同群体的用户提供差异化产品和服务。

    21世纪，得益于信息传输、计算能力的快速发展，此阶段强调基于数据的用户行为分群，越来越多的数据被用于建立用户分群模型，而这里的分群模型就是聚类模型。

    所谓聚类模型，大致的逻辑是，将样本点根据某种特征进行分类，达到的效果是，类与类之间的差异大，而同一个类内的用户差异较小，从而达到分群、定类别的目的。

    聚类分析常常用于商业用户细分，区别于传统的、无差别的不区分用户的营销理念，进行用户细分可以深入了解和认识各群体的用户，从而制定更加有效的用户管理策略和更有针对性的营销手段。

1、用户细分的重要意义

    对用户进行细分有利于深入洞察用户需求、提高业务运营效率和效益、降低运营风险、保持业务的可持续增长。

    对用户细分的检测也是了解市场、预测未来变化趋势的主要方式。

2、用户细分的不同商业主题

    根据不同的商业主题，常见的分群有4种类型，分别用于产品设计、用户管理、用户营销和资源投入优化的需求。

1）产品设计阶段的用户细分

    一个产品可以为不同的用户群体提供服务，比如一个宠物托管产品的用户群体可以分为退休驴友、北漂驴友、怀孕准妈妈、白领商旅人士等不同的群体，这些群体对宠物托管这个产品的特性提出不同的要求。

    由于产品还处于研发期，很难通过自动化数据采集工具获取用户数据，因此这类用户分群往往采用人类学分析方法和调研问卷方法，寻找需求、态度和痛点。人类学分析的目的是充分融入潜在用户的生活和工作场景，与用户产生共情，此阶段会使用用户同理心地图这个工具。

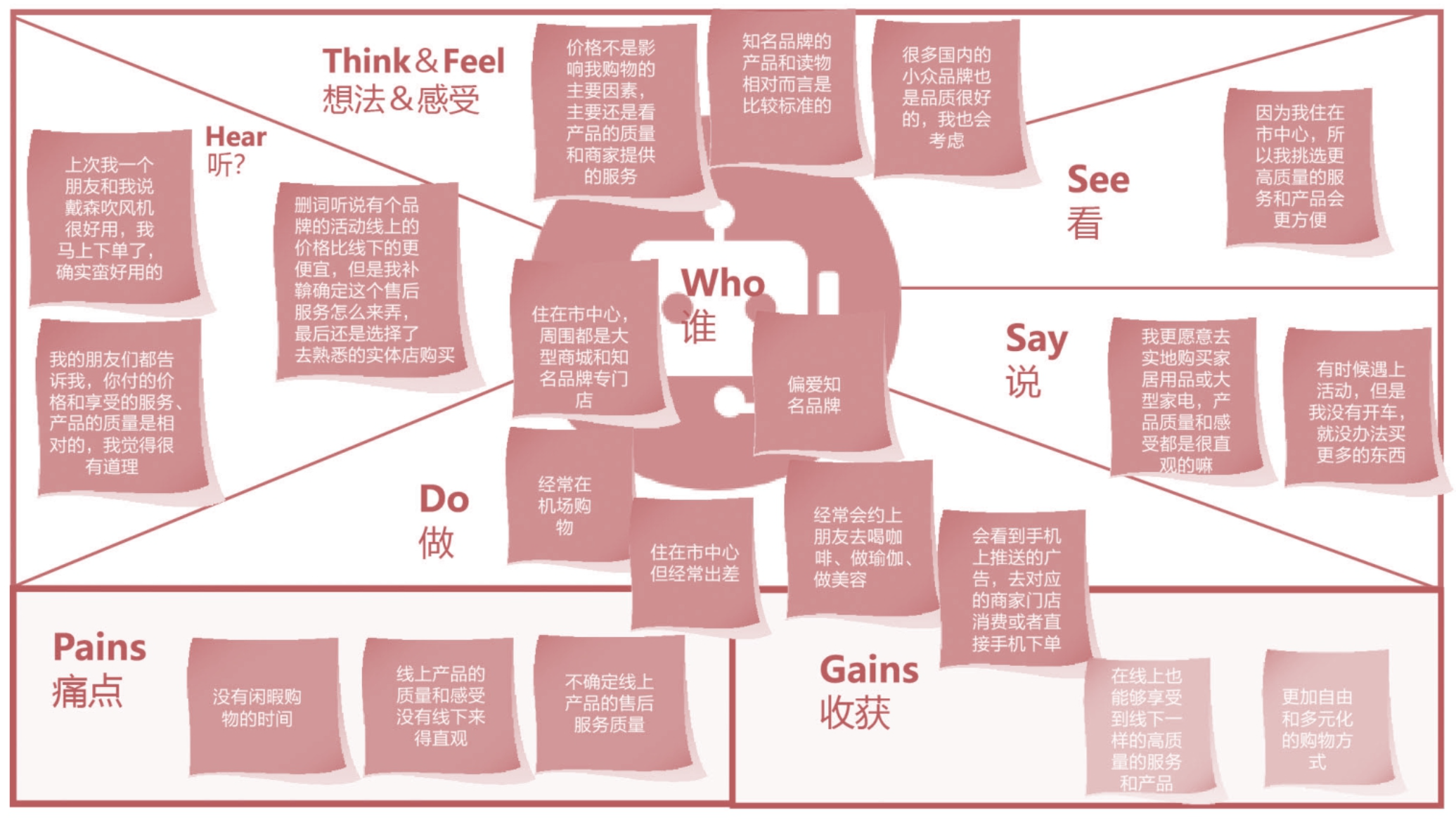
    用户同理心地图分为两部分，上半部分划分了5个象限：听、做、说、看和想（想法、感受），用来模拟用户的大脑，思考用户的动机；下半部分是随着讨论的进行，最终获得的痛点和收获。

    用户同理心地图是单个用户层面的，产品的特性设计需要从单个用户层面进行抽象，获取某类群体的共性，这时可以使用亲和图对单个用户进行聚类。

    图所示是一家宠物托管公司根据用户同理心地图获得用户的痛点所做的亲和图。

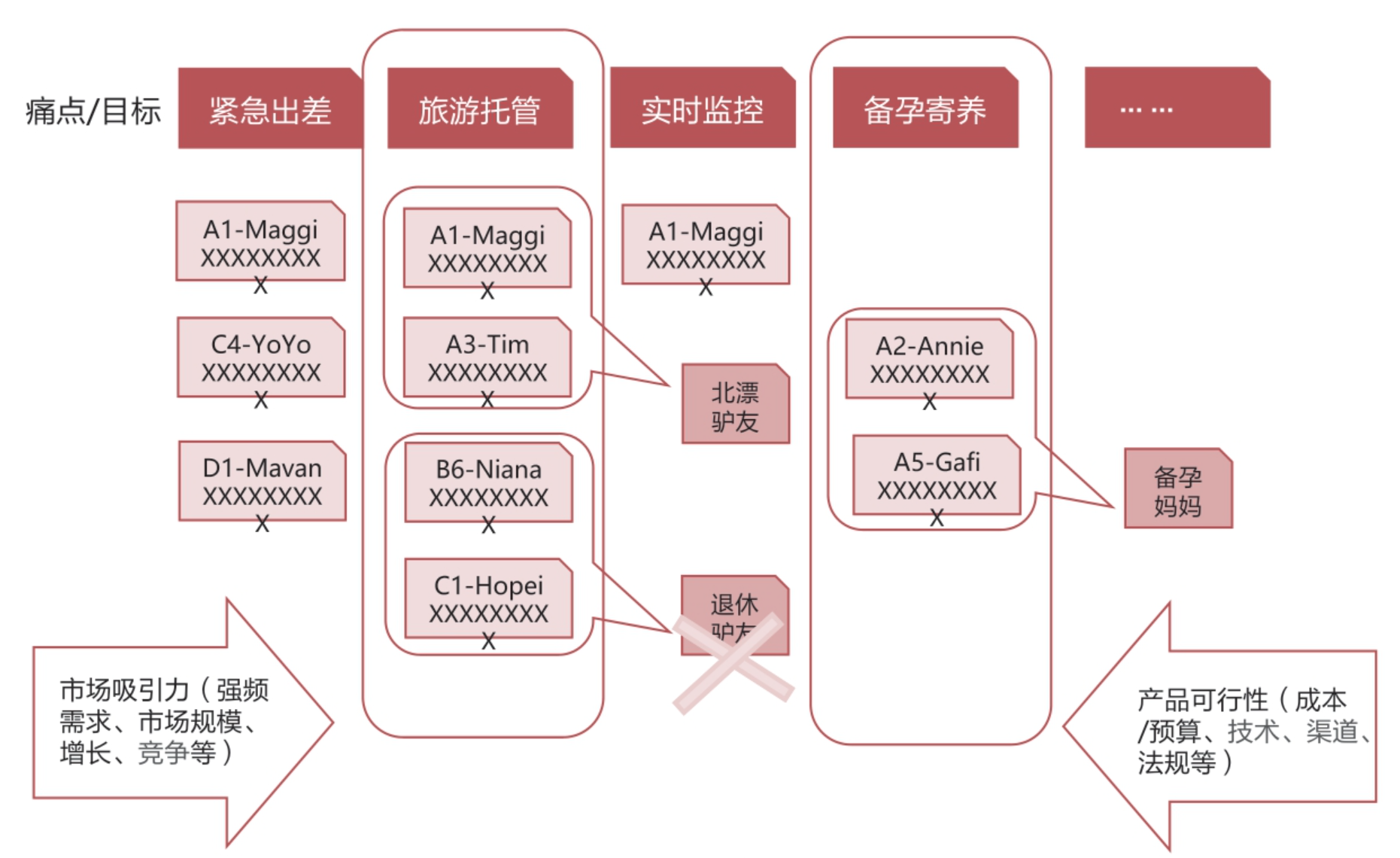
    这家宠物托管公司把其用户托管的目的分为紧急出差、旅游托管、备孕寄养等，根据亲和图，对用户进行聚合，如北漂驴友、退休驴友在宠物托管需求上被划为一类，即旅游托管。

    根据市场吸引力、产品可行性等要素，选出那些可以被用来重点关注的用户，这些典型用户的痛点可为产品设计做参考。

2）资源投入优化-用户价值分层

    用户价值分群是指依据用户的当前价值或潜在价值进行分群，多是基于业务规则对用户进行分群，潜在用户价值分群最常用的方法就是RFM模型。

    RFM模型是根据用户的3个维度进行价值区分的，分别是消费热度、消费频率、消费金额。RFM模型中的R表示最近一次消费的时间间隔，F表示消费的频率，M则表示消费的金额。

    第一步：在数据库中拉取相关数据，数据字段包含用户码、产品类型、消费时间、消费金额，用于计算每个用户的R、F、M值，如图：

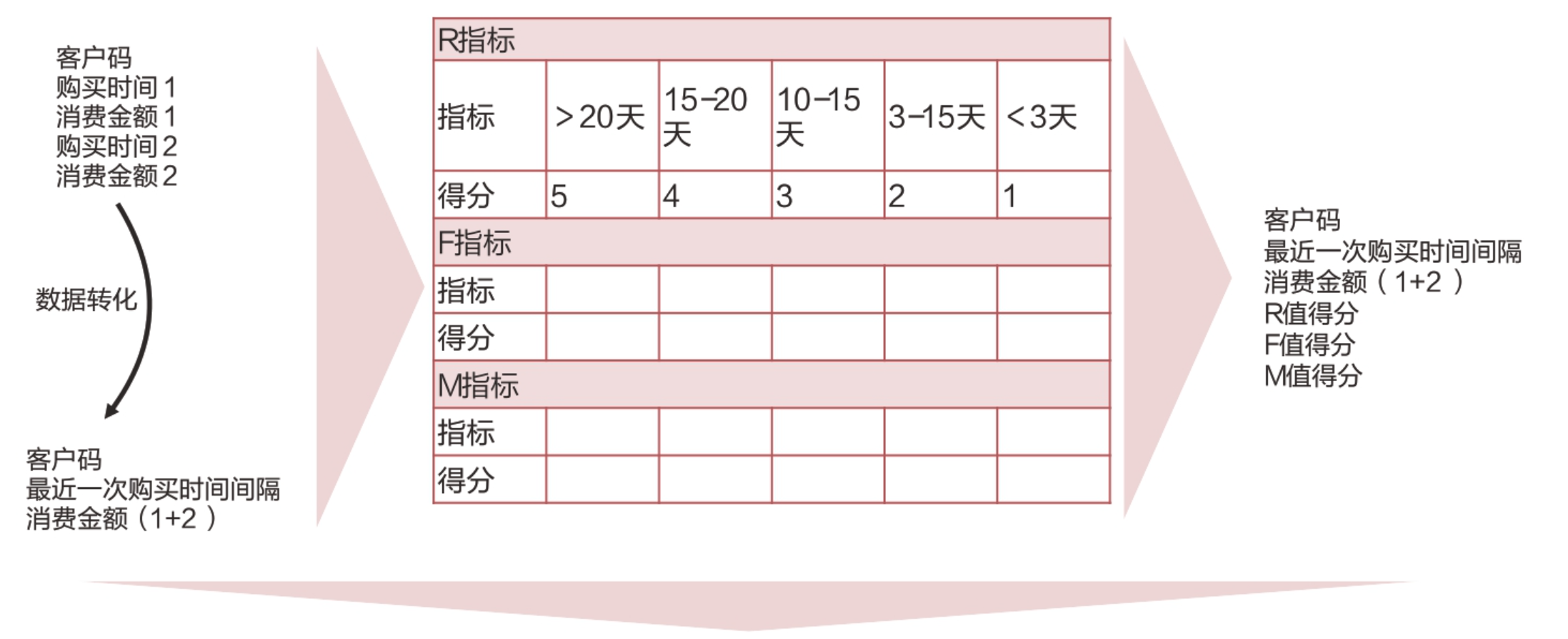
    第二步：分别将F、M的值与其对应的平均值做比较并打分，对R的打分可以制定合适的天数阈值，如这里把距离上次购买超过20天的R指标打为5分，小于3天的打1分。

    第三步：根据相应的R、F、M取值来确定一个用户的价值分层，如图

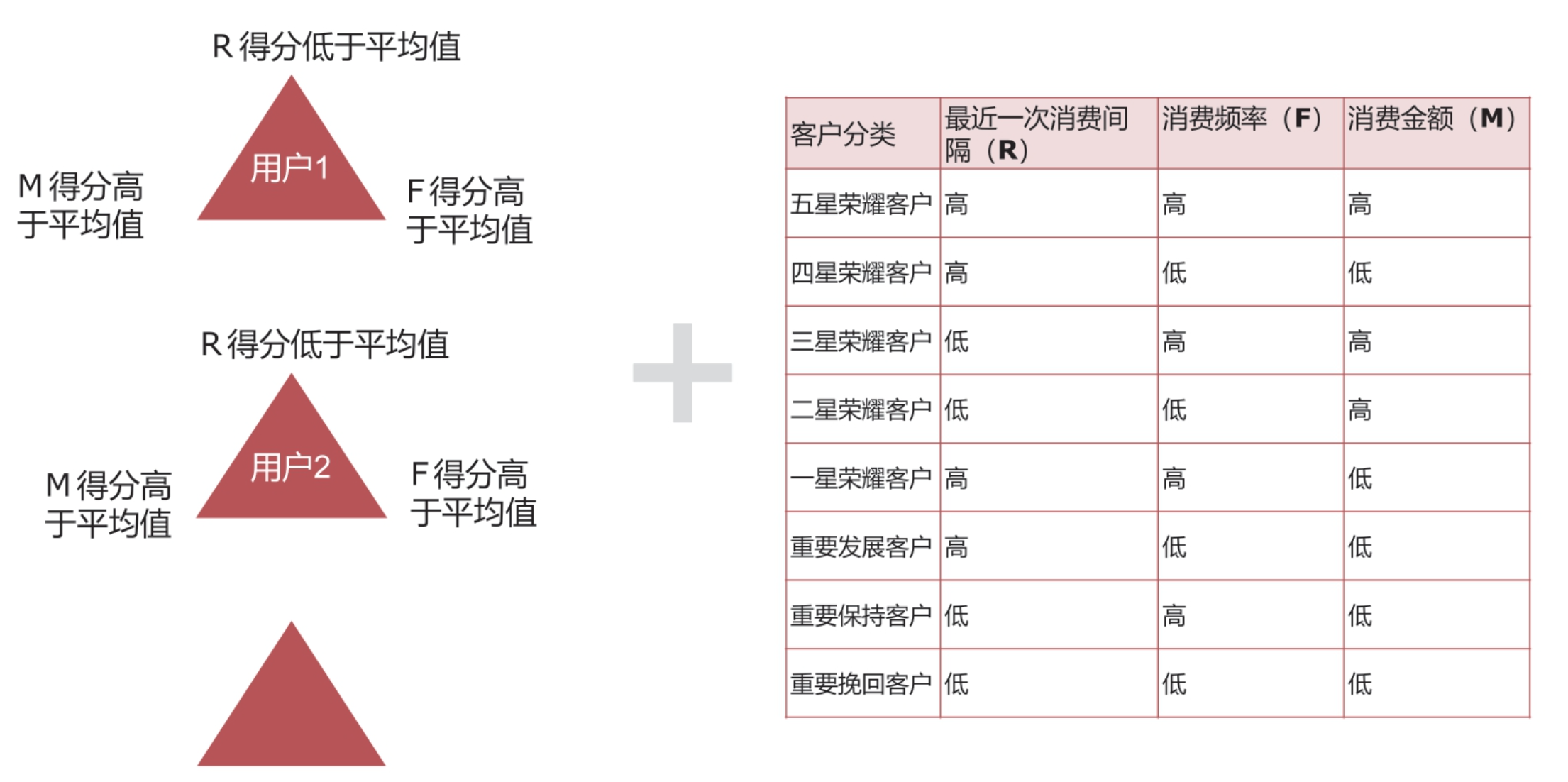
    如果一个用户，其R、F和M的值都高于平均分，即近期消费、高频率、高消费，则是对公司价值最大的用户，称为五星荣耀用户，其他用户同样可以根据这种规则依次进行价值分层。

3）用户管理-用户生命周期分群

    生命周期，这个概念借用了人类生命的整个过程，即一个人会经历诞生、生长、成熟、衰老和死亡的过程。对于企业而言，用户也有类似的生命周期：潜在用户阶段、响应用户阶段、既得用户阶段和流失用户阶段。

    图是一家电信公司针对用户不同阶段的营销管理方法：

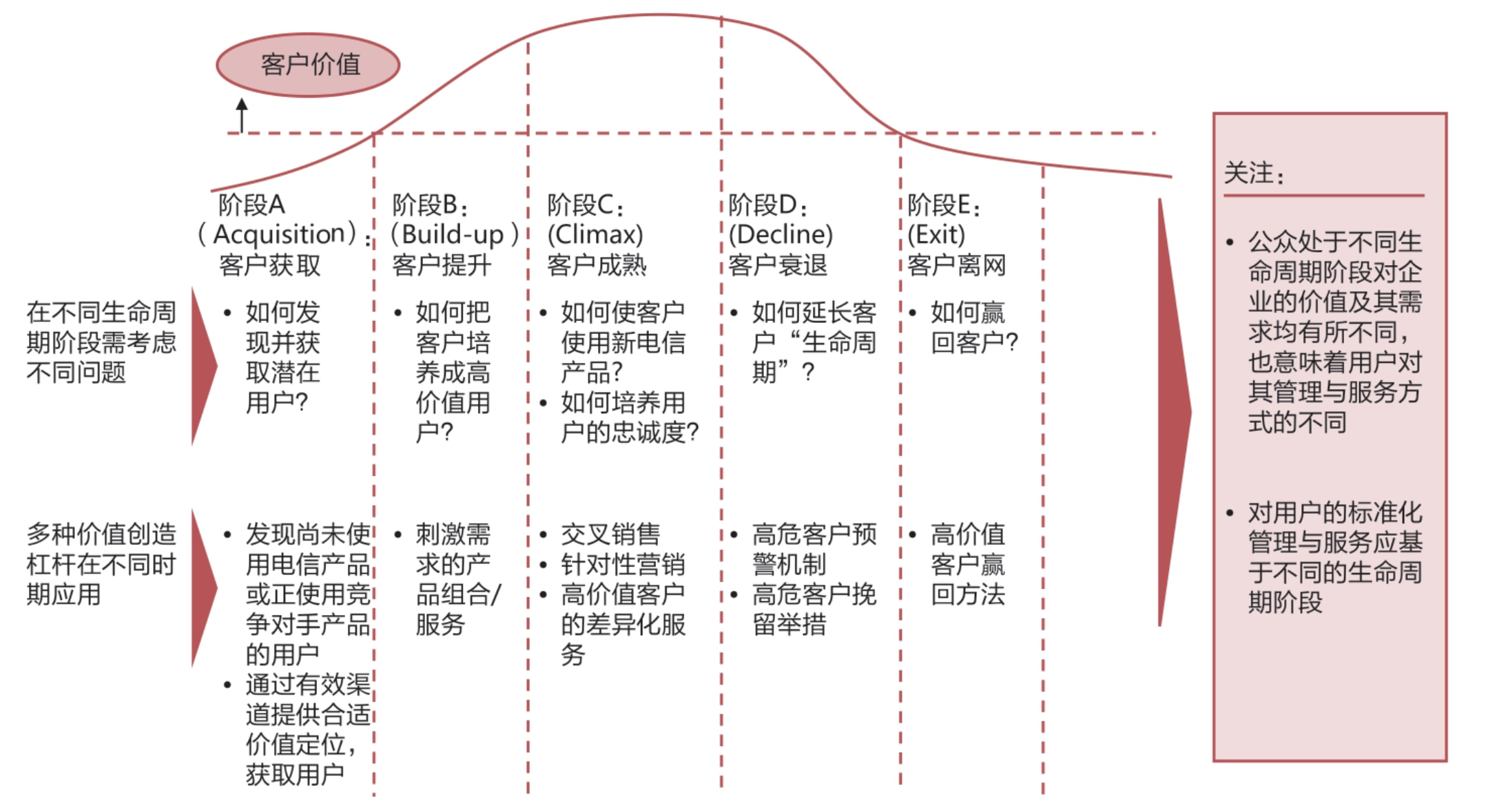
    比如，在用户成熟阶段（既得用户时期），要考虑如何让用户使用新的电信产品，如何培养用户的忠诚度等，方法有很多，如使用关联规则进行交叉销售来提高产品的购买率，或者针对性地营销、对高价值用户进行差异化服务等措施。

4）用户营销-用户行为特征分群

    根据用户的行为数据用聚类等算法进行分群，用来做营销。

    图所示是根据循环信用次数和交易次数这两个维度，对信用卡用户进行聚类分群的：

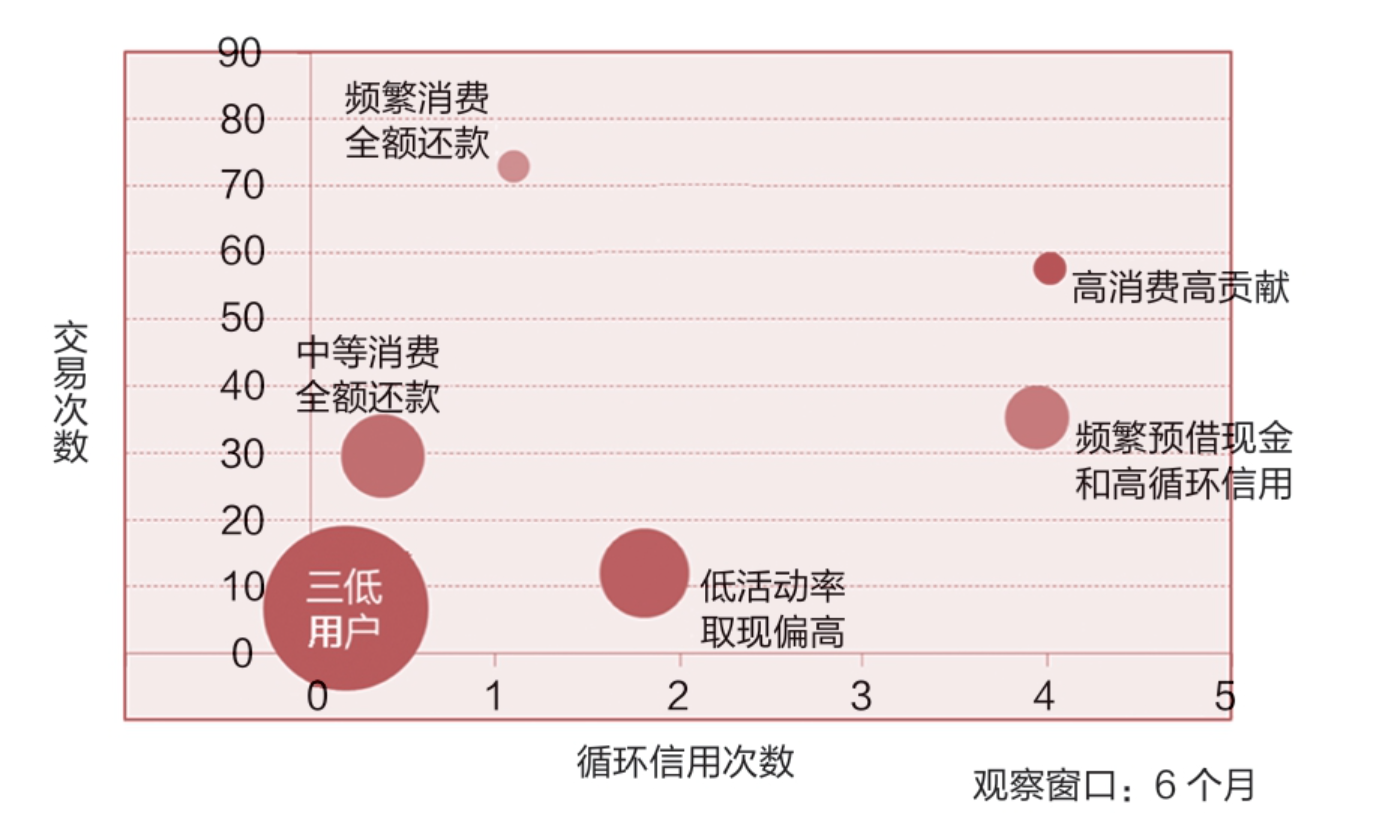
    针对不同行为特征的用户群体，为其概括性地取一个群名称，并且根据用户需求进行针对性的营销。

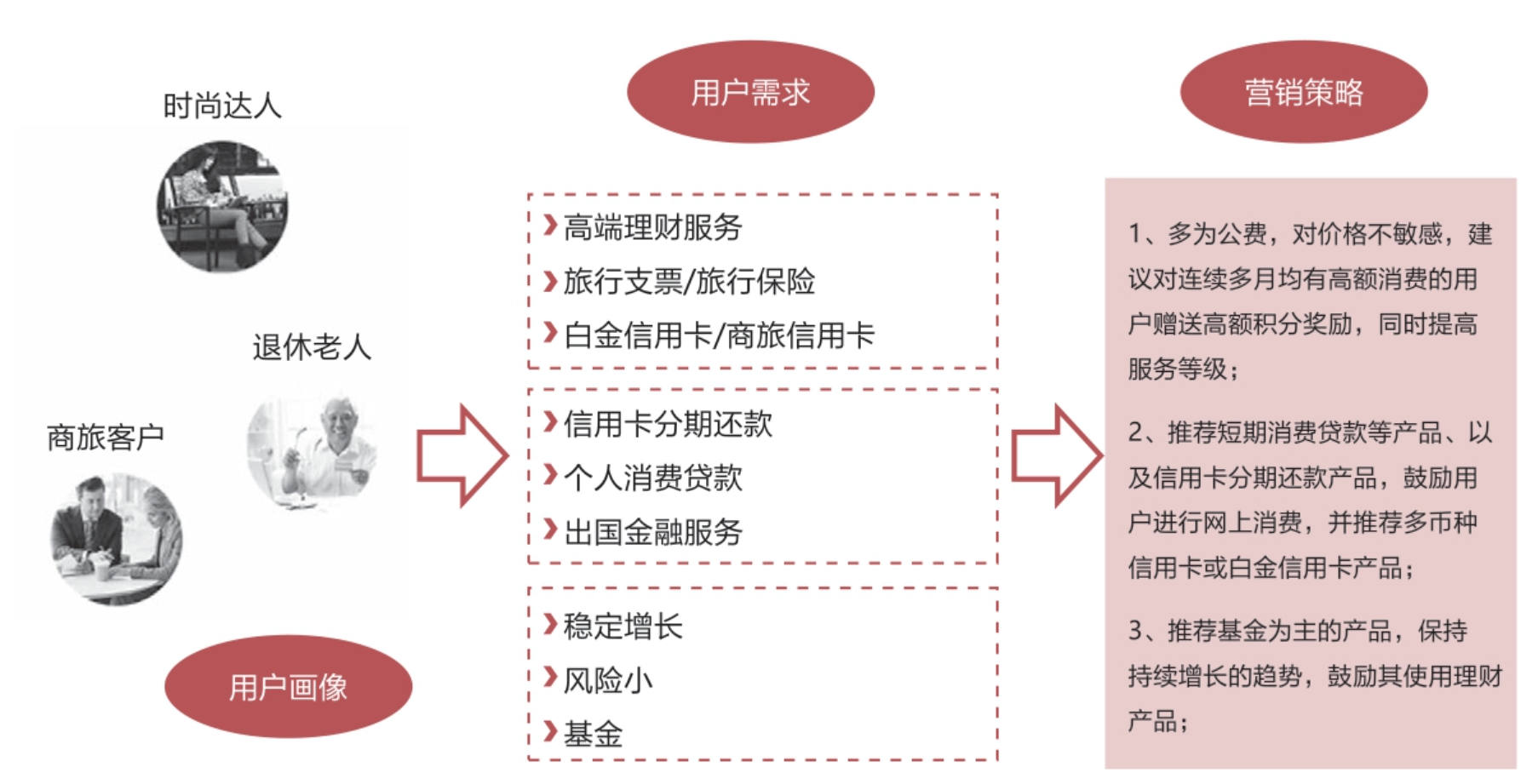
    下面举一个保险产品公司根据消费行为进行用户分群的例子来理解聚类等算法对用户行为特征做用户细分这种思想。

    下图是一家保险产品公司结合公司积累的用户数据和专业咨询公司基于数据聚类分群后的群体画像。

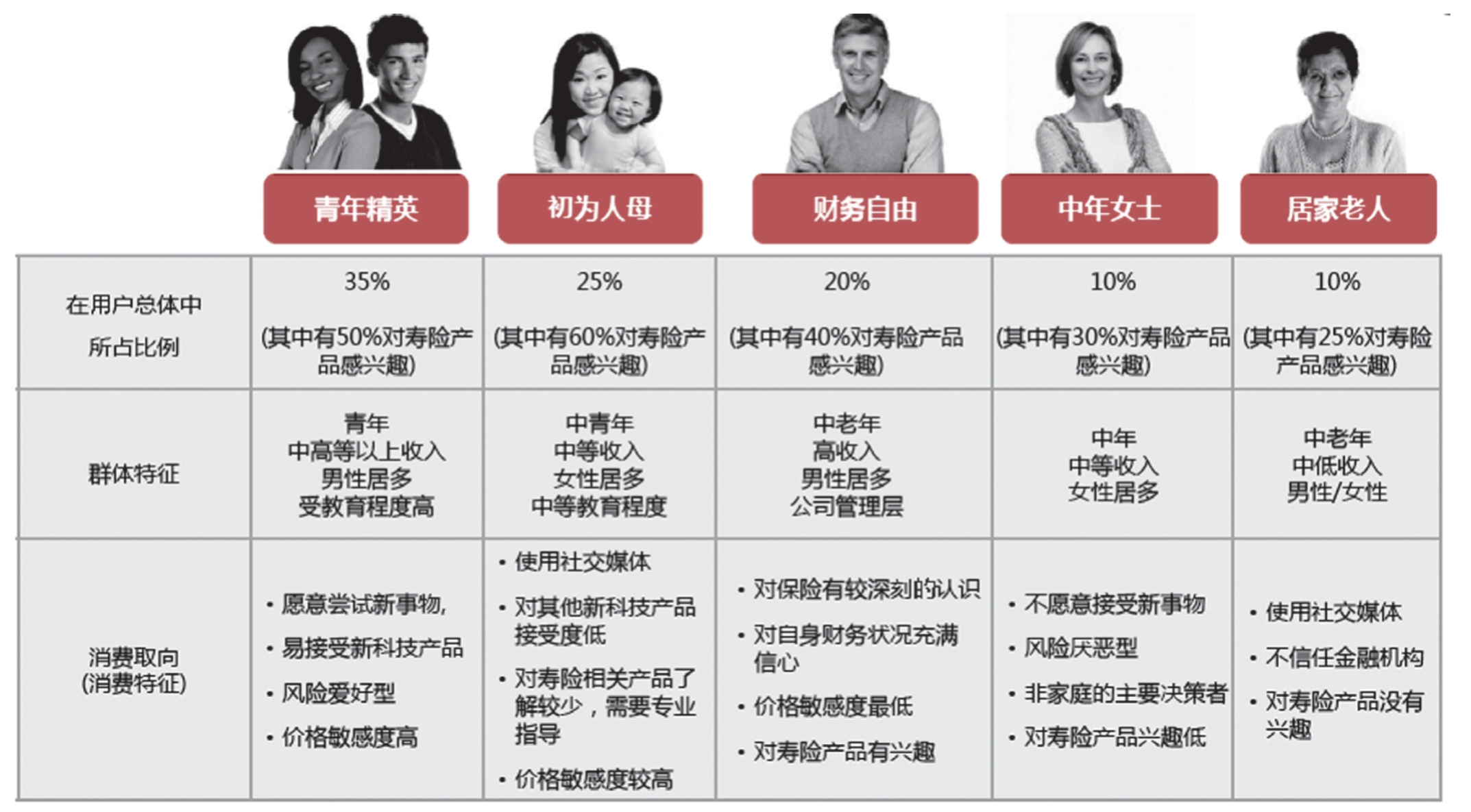
    在用聚类模型做用户细分用于营销时，我们希望每类群体的用户比差距不要太大，因为单独群体比例很小是不方便营销的，不可能单独花费精力和资金去维护比例很小的一个群（注意，这里并不是说比例很小的用户价值就小），这样的分群是不合理的。在本例中，我们看到每个群的人群占比从大到小排列，最大的用户群占总用户群的35%，最小的用户群如居家老人，也有10%的比例，与最大值35%差距也没大到离谱的程度。

    事实证明，在基于多维度数据的、科学的用户分群基础上的营销策略要比基于主观或局部信息的营销策略更能把握用户，进而达到有效营销的目的。

    总的来说，以产品线的角度分析，用户分群有如下所示的商业应用价值：

二、聚类分析的基本概念

    行为特征用户细分简单来说就是将现有的消费群体按照一定的规则分成若干个小群。分群目标是，使得每个群的特征描述明确且具体，不同群之间的特征差异明显。这跟聚类算法的逻辑是一样的，即通过对数据进行分类，使得类与类之间的差异大，而同类内的样本差异小，从而达到分群的效果。

    差异其实就是相似度的衡量，不同的算法有不同的角度，就聚类算法而言，差异经常使用距离这个概念去量化。

    计算样本点之间的距离，通常有多种方法。假设有两个观测（两点），均用向量表示，第i个观测值为Xi～(xi1, xi2, …,xip)，第j个观测值为Xj～(xj1, xj2, …, xjp)，下面用具体的数据点表示，如图

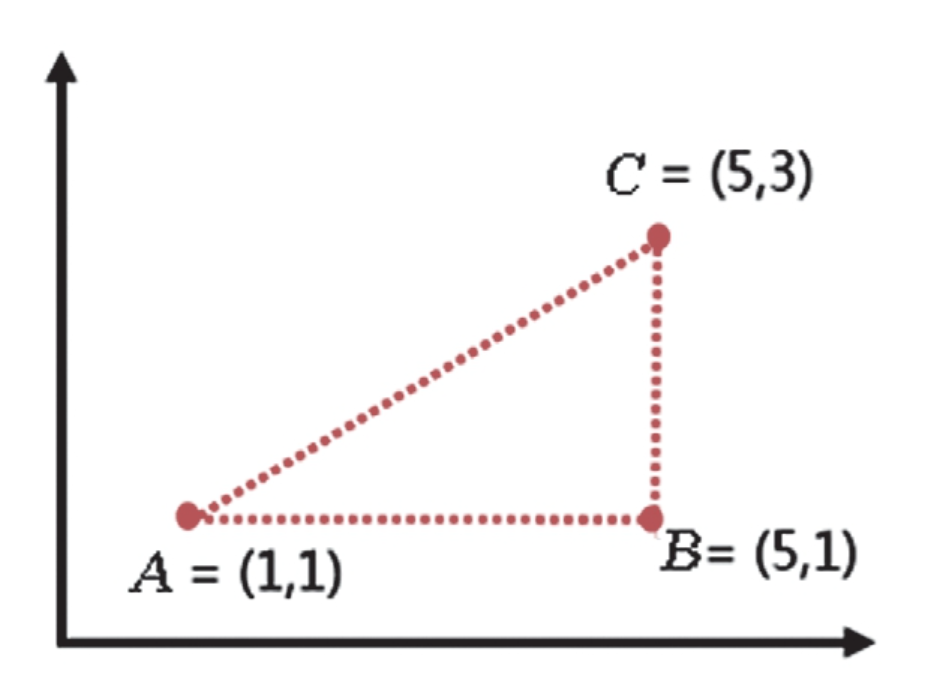
    A观测的坐标是(1, 1)，B观测的坐标是(5, 1)，C观测的坐标是(5, 3)，计算两个观测之间距离的方式有很多种，常用的距离表示方式如下。

    绝对值距离：

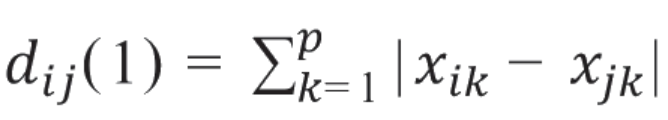
    欧式距离：

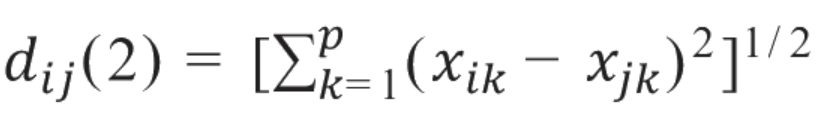
    明考斯基距离：

    当明考斯基距离的q=2时，就是欧式距离。在层次聚类和Kmeans聚类中，计算点与点之间的距离通常使用欧式距离，如在本案例中，A点和C点的欧式距离计算为：(5-1)²+(3-1)²=16+4=20，则A与C距离为20^1/2。

三、聚类模型的评估

    聚类是一种无监督方法，无因变量，其效果好坏难以在建模时使用有监督模型的评估方法衡量。

    不过可以在建模之后，通过外部数据验证聚类效果的好坏。比如，将聚类后的标签作为“以下哪个选项更贴近您”的问题选项让用户自己填写，然后用准确度或ARI等指标进行评估。不过这样做的成本较高，也有一些低成本、精确度尚可的指标用于衡量聚类效果，其思想在于类簇内的差异尽可能小，而类间的差异尽可能大。评估聚类模型优劣的主要标准有轮廓系数、平方根标准误差和R²。

1、轮廓系数

    样本轮廓系数：

    整体轮廓系数：

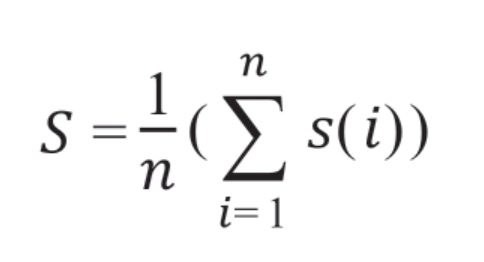
    其中，a(i)表示观测i到同一类内观测的距离的均值，b(i)表示观测i到不同类内所有观测的距离的均值最小值，S(i)表示观测i的轮廓系数。

    生成聚类结果以后，对于结果中的每个观测来说，若a(i)小于b(i)，则说明该观测在聚类的类簇中是合理的，此时，如果 a(i)/b(i) 的值越趋近于0，那么S(i)的值越趋近于1，聚类效果越好；若a(i)大于b(i)，则说明该观测还不如在别的类簇中，聚类效果不好，此时 a(i)/b(i) 的值趋近于0，而S(i)的值趋近于-1；若a(i)=b(i)，则说明不能判断观测i在哪个类簇中效果好，此时S(i)的值为0。

    所以，S(i)的值域为(-1, 1)，其值越小表示聚类效果越差，其值越大表示聚类效果越好。将所有观测的轮廓系数值相加并求均值，就可以得到整个已聚类数据集的轮廓系数，同样，衡量其聚类好坏的标准与单个观测的轮廓系数的衡量方式是一致的。

2、平方根标准误差

    平方根标准误差(Root-Mean-Square Standard Deviation,RMSSTD)的计算公式如下：

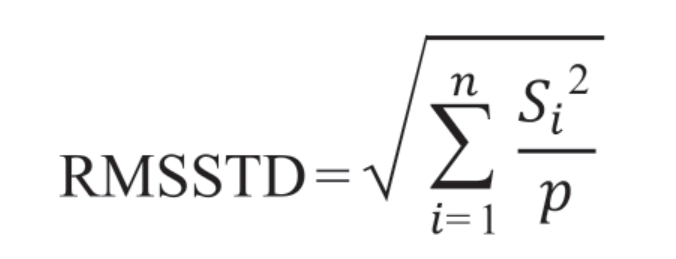
    其中，Si表示第i个变量在各群内的标准差之和，p为变量数量。群体中所有变量的综合标准差，RMSSTD的值越小，说明群体内（簇内）个体对象之间的相似程度越高，聚类效果越好。

3、R²

    R²(R-Square)的计算公式如下：

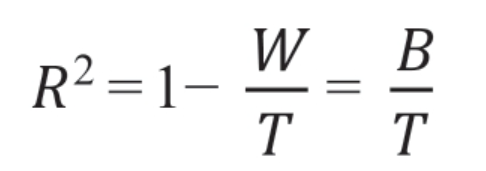
    其中，W表示聚类分群后的各群内部的差异程度（群内方差），B表示聚类分群后各群之间的差异程度（群间方差），T表示聚类分群后所有数据对象总的差异程度，并且T=W+B。

    R²表示聚类后群间差异的大小，也就是聚类结果可以在多大比例上解释原数据的方差。R²越大，说明群内（簇内）的相异性越高，聚类效果越好。

4、ARI

    当聚类结果有“标准答案”时，可以使用ARI(AdjustedRand Index)评价聚类效果，计算公式如下：

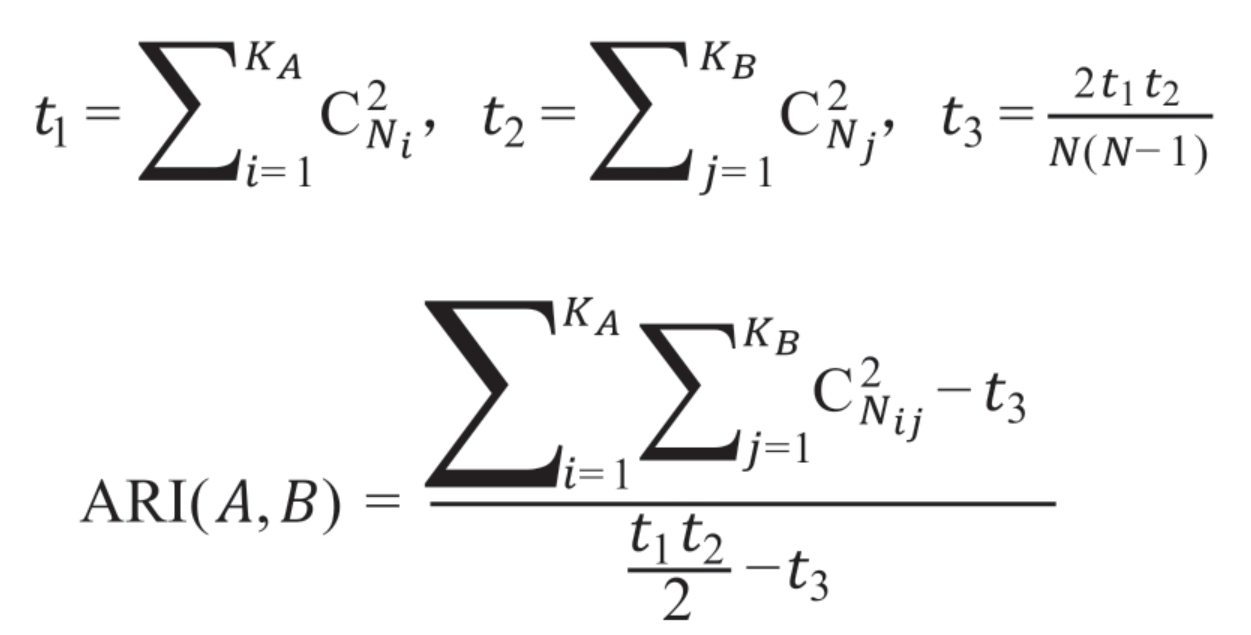
    其中，A和B是数据集Z的两个划分，分别有KA和KB个簇；N_ij表示在划分A的第i个簇中数据的同时也在划分B的第j个簇中数据的数量；N、N_j分别表示划分A中第i个簇与划分B中第j个簇的数据的数量。

    若ARI(A, B)=0：则划分A和B是独立的。若ARI(A, B)=1：则划分A和B是完全相同的。ARI的值越大，说明聚类效果越好。

四、层次聚类

    按照不同的角度（比如基于划分、基于层次、基于密度、基于网络），聚类有很多不同的算法，层次聚类（也被称作系统聚类）是基于层次的聚类方法，因为这种方法在聚类过程中能够形成类相似度层次图谱，便于确定类与类之间的划分，所以该方法能够得到比较理想的类的数量，是目前商业应用使用较多的一种聚类算法。

1、层次聚类的算法描述

    层次聚类的思想：首先把n个样本视作n类，使用观测之间的距离公式计算两两观测之间的相似性，把距离较小的两类合并为一个新类，再按照某种方法计算类与类之间的距离，然后继续将距离较小的类合并到新的大类，重复上述过程，直到所有的样本都分到一个类。

层次聚类算法的一般步骤如下：

(1)假设有n个样品，每个样品被单独看成一类，即构造n个类，每个类包含且只包含一个样品。

(2)计算n个样品两两之间的距离，以及类间距离矩阵，并将距离最近的两类合并为一个新类。

(3)计算新类与当前各类之间的距离。

(4)一直重复上述过程，直至所有的观测被聚为一类，并绘制聚类图。

(5)决定聚类数目和类别，并对类作出解释。

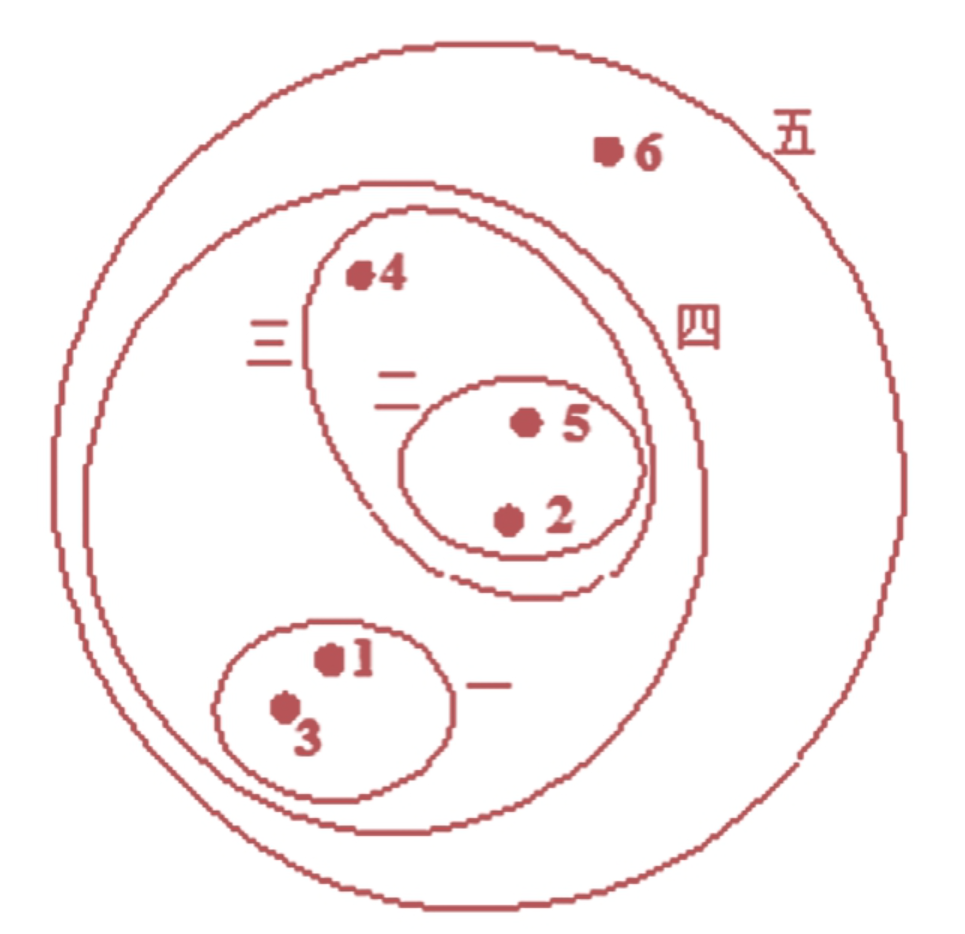
    在系统聚类算法中，首先把6个点单独看成一类，即现在有6个类，计算类与类之间的距离（点与点），把距离较小的两个类合并成一个新的大类，如这里类1和类3距离较近，合并成新的大类一，新的大类一继续参与其他类的距离计算，这样不断地计算和合并，直到所有的样本都被划分到一个类中，这里6个点都被划分成一个类五。

    类与类之间距离的衡量，常用的一些计算方法：

(1)重心法（平均法）

    重心法计算的是观测类各自重心之间的距离，左边的类有3个样本点，使用这3个点的重心代替这3个点去计算类与类之间的距离，也就是计算重心与重心之间的距离，这里重心的确定其实就是求每个类中所有点的均值。重心法的特点是很少受到异常值的影响，但是因为类间的距离没有单调递增的趋势，所以不适合在层次聚类中使用层次聚类图观察分群的结果，聚类图上可能会出现图形逆转，计算起来比较麻烦。

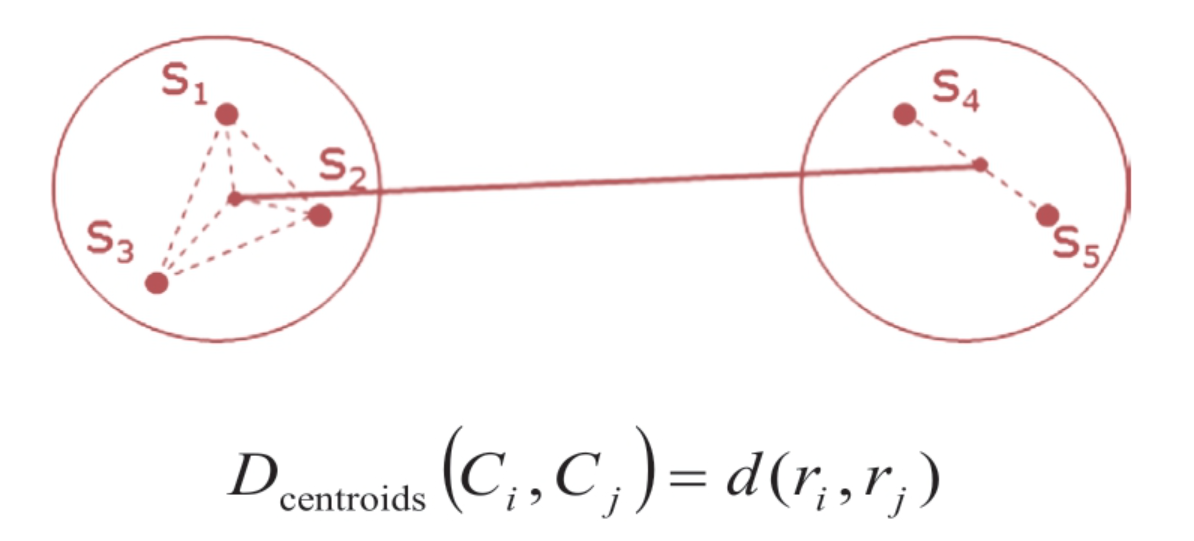
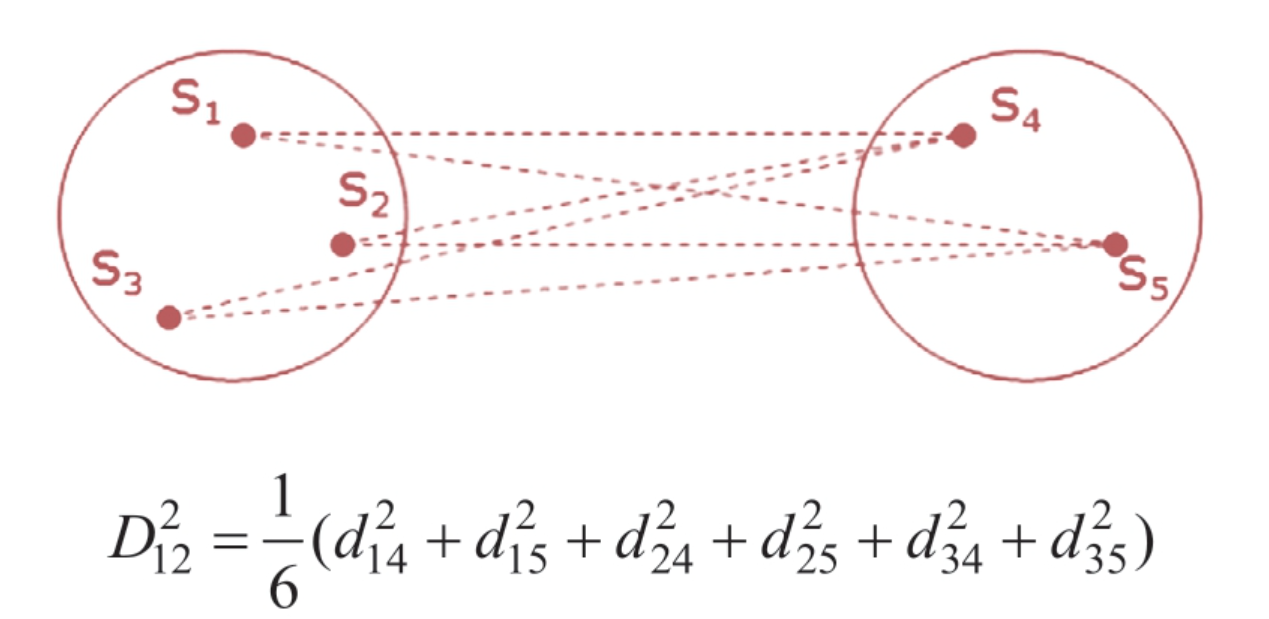
(2)全联接法（平均联接法）

    考虑一类中所有样本点与另外一类中所有样本点两两之间的距离，用距离的平方和再求平均。案例中的就是求s1到s4的距离的平方。案例中的点两两联接，一共有6条线，求平均是为了去除次数的影响；但是因为这种计算方法会考虑所有样本点的距离，所以该方法对异常值比较敏感，结果不够稳定。

(3)Ward最小方差法

    Ward最小方差法可以计算两簇内观测的方差，并计算合并两簇后大簇的方差，后者减去前者得到方差的增量，当所有的簇中某两簇合并方差增量最小时，说明这两簇的合并是适合的，方差增量的计算公式为：

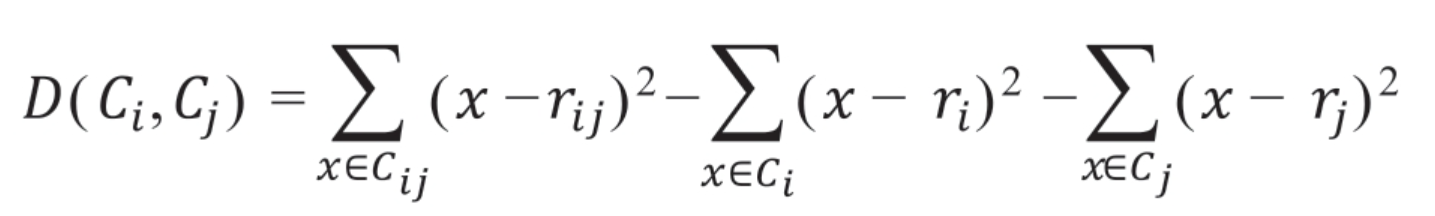
    其中，表示簇i的方差；表示簇j的方差；表示簇i与簇j合并后的方差，该方法很少受到异常值的影响，在实际应用中的分类效果较好，适用范围广。但该方法要求样本间的距离必须是欧氏距离。

    Ward算法的计算步骤：

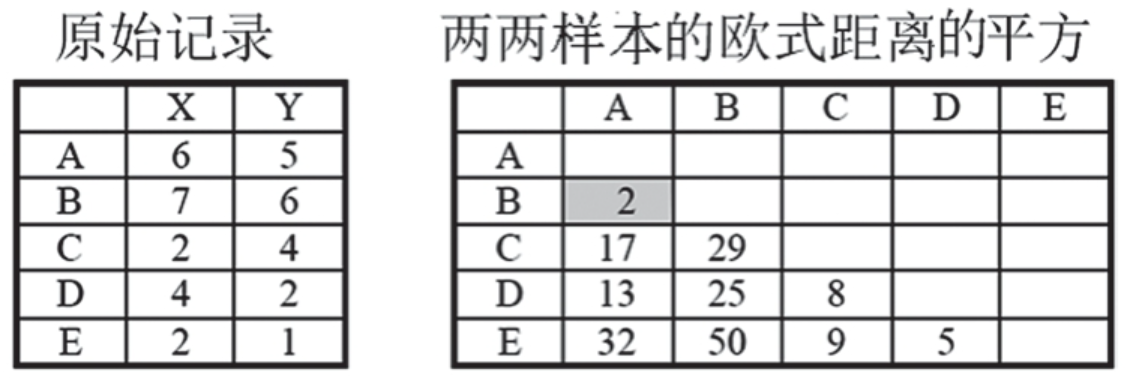
    根据欧氏距离，A、B首先应被归为一类，下面看看根据Ward最小方差法A、B是否也被归为一类。在聚成四类时，假设A、B被归为一类，则组内离差平方和为：

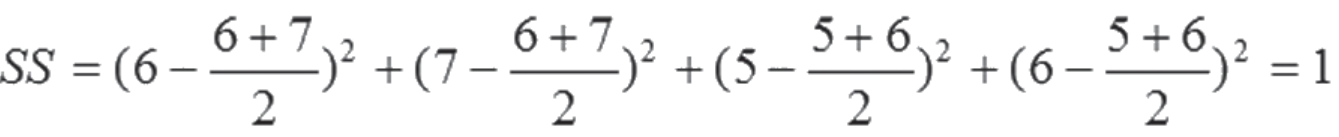
    同理，如果C、D被归为一类，则组内离差平方和为：

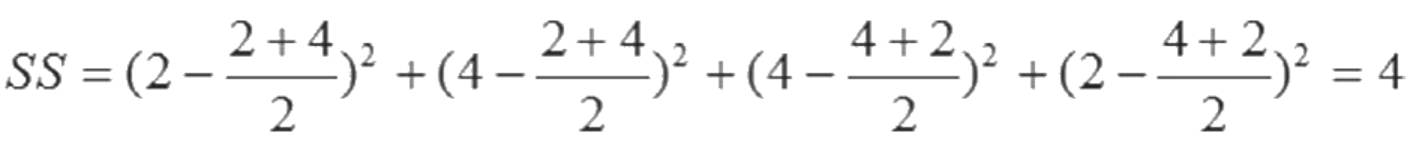
    其他方案与此类似。在聚成四类时，组内离差平方和如图：

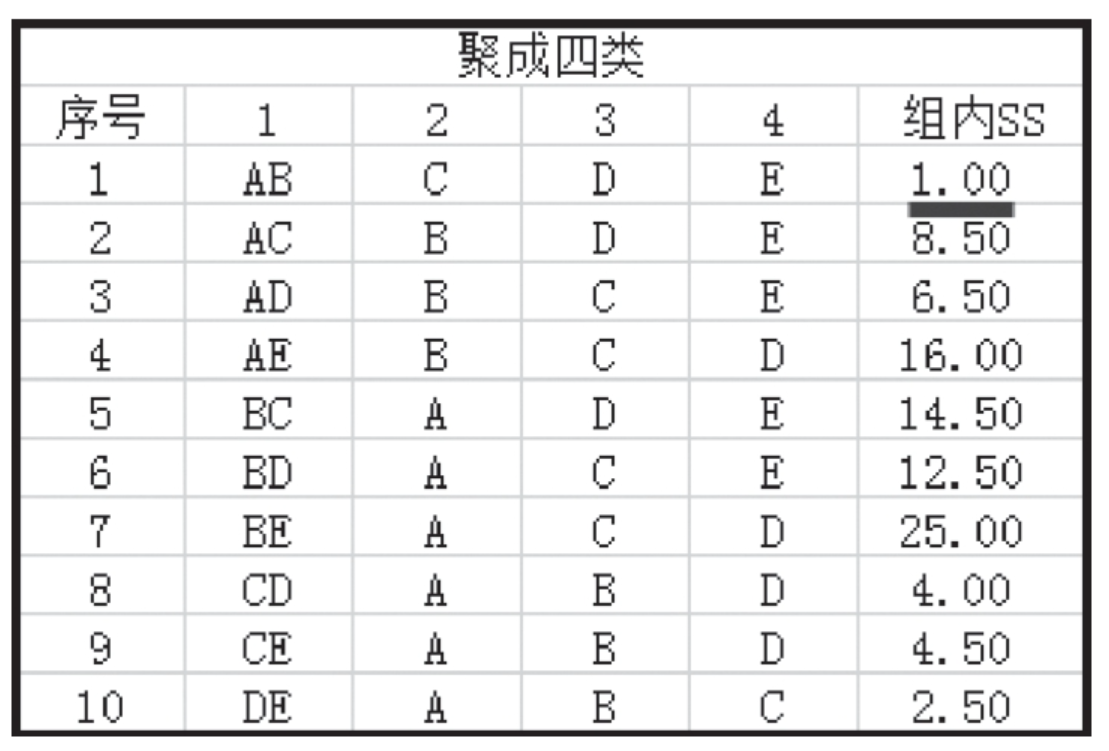
    从结果来看，在聚成四类时，A、B被归为一类是最优的，因此Ward最小方差法和欧氏距离法的结论是一样的。

    当聚成三类时，因为前面已经确定A、B被归为一类，所以接下来遍历所有可能的组合情况，比如AB、CD、E组合，组内离差平方和SS=1+4+0=5，如图：

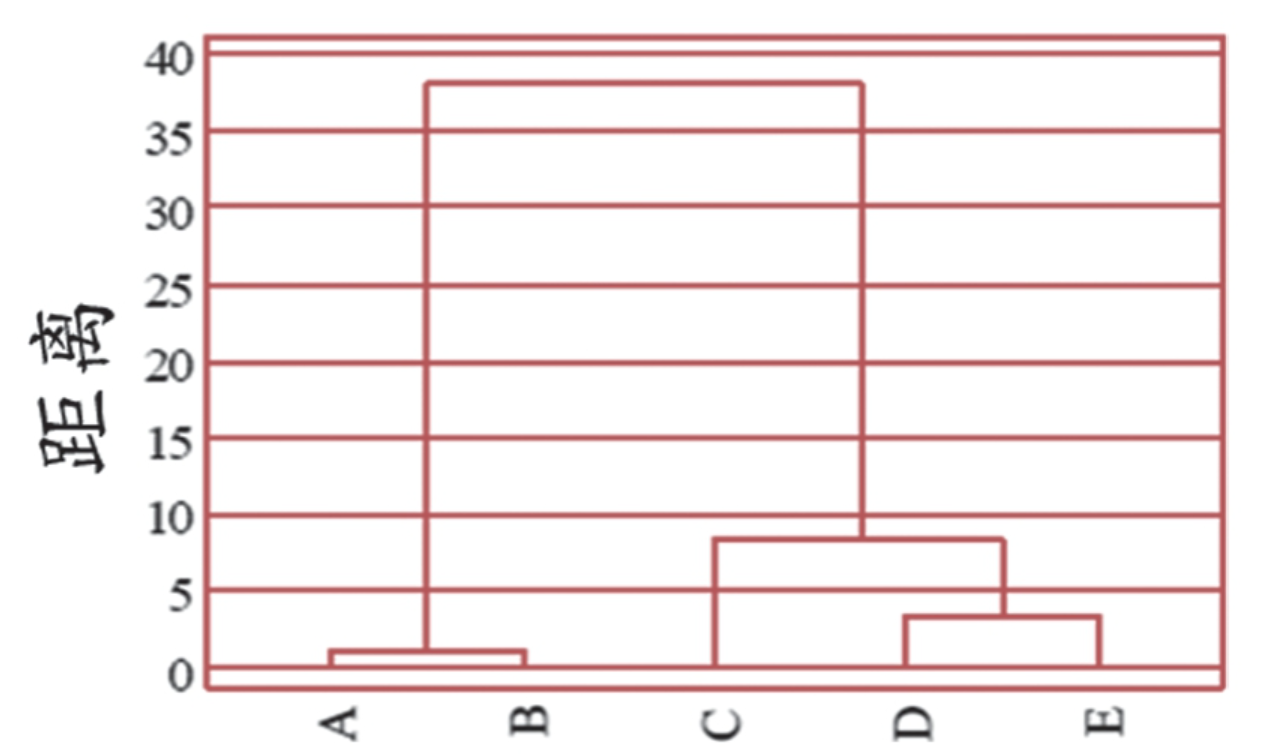
    最终的聚类结果：首先A、B聚为一类，然后D、E聚为一类，接着C、D、E聚为一类，最终全部聚为一类。

    最合理的聚类结果是聚为两类，即A、B一类，C、D、E一类。因为从两类到一类之间的组内离差平方和变化最大。

 Ward最小方差法聚类的树型

2、层次聚类分群数量的确定

    层次聚类的优势是，可以根据层次聚类图（聚类谱系图）来确定样本的分群个数。这种自上而下的、类似决策树的谱系图不仅能帮助我们选择合适的群，还能让我们知道哪些样本点被分到了哪个群。

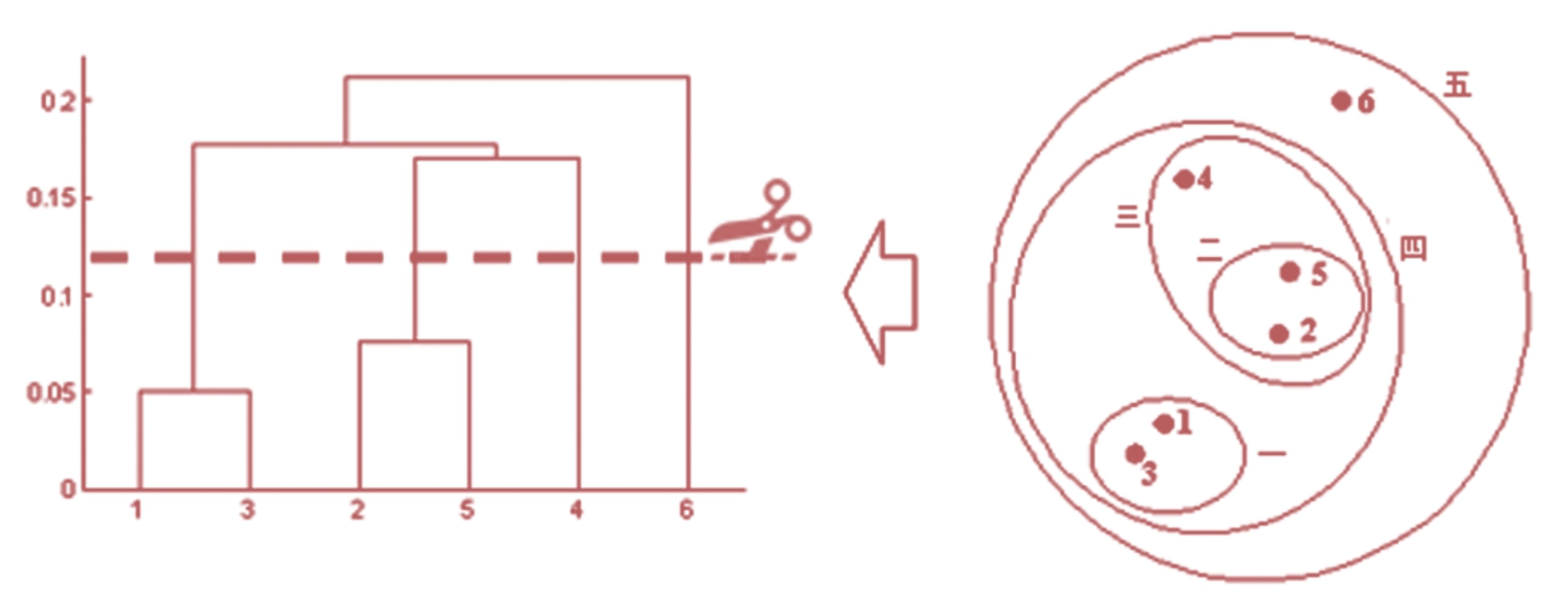
    横轴表示各个样本点的标签，这里一共有6个点。纵轴表示聚类的距离，找到最长的“树枝”（类似鱼叉的形状），从“树枝”上横向画一条直线，得到几个交点就表示分成几个群，如这里层次聚类图告诉我们分成4个群比较合适，即点1和点3合成一个群，点2和点5合成一个群，点4、点6各自单独一个群。

3、层次聚类应用简单案例

    项目的需求是，评价各个省（市）的经济发展水平，哪些省（市）是类似的、水平相当的。

4、层次聚类的特点

    层次聚类的优点：具有较好的解释性，分析人员可以通过层次聚类图确定需要将处理的样本数据分成几类，以及这些类的样本有哪些。

    层次聚类的缺点：层次聚类处理大样本数据较为吃力，需要不断计算点与点的距离及类与类的距离，对计算机的计算和存储能力、计算时间都是一个挑战。

    面临大样本数据，有没有快速聚类的方法呢？K-means聚类就是比较快速的聚类方法。

五、K-means聚类算法

    其基本思想是以迭代为理论基础，先对样本观测进行粗略分类，然后按某种最优准则逐步修改分类，直至最优为止。K-means聚类算法是聚类分析中的常用方法，常用于用户分群。

1、K-means聚类算法描述

K-means聚类算法就是计算样本点与类簇质心的距离，与类簇质心相近的样本点被划分为同一类簇。

K-means聚类算法大致分为4个步骤：

(1)设定K值，确定聚类数，软件随机分配聚类中心所需的种子，如图

(2)计算每个观测到类中心的距离（欧式距离或明考斯基距离），并分成K类，如图

(3)把K类中心（均值）作为新的中心，重新计算距离，如图

(4)迭代到收敛标准为止。

2、K-means聚类算法的应用：用户细分

    由于K-means聚类算法随机选取中心点且聚类快速的特点，因此该方法常用来处理大样本需求的聚类。在商业应用中，该聚类算法常用来做用户细分、用户分群。下面通过一个具体的案例进行说明。

1）项目目的

    某银行想通过交易行为数据将该银行的用户进行分群，便于为具有近似行为特征的用户提供一些标签，也为其他算法模型提供基础，提高相应模型的精度。

2）数据解读

    该银行交易行为数据有4个特征，分别表示去柜台服务、使用ATM的次数、刷POS机的次数和使用信用卡的次数。导入数据，代码如下：

3）数据预处理

4）建立聚类模型

六、聚类事后分析：决策树应用

    可是对于业务营销而言，光知道结果是不行的，中间的过程是怎么来的？为什么这些用户被分到了某个群呢？到底是基于哪些特征划分的呢？这些同样是使用聚类算法得到分群后我们所关心的，即聚类的事后分析。

    决策树算法的决策树图能够很好地帮助我们得到划分的过程。

1、决策树的基本概念

    决策树算法在机器学习算法内被划分为有监督的学习算法。决策树算法发展很成熟，根据对属性划分方法的不同，决策树可以分为基于熵的ID3决策树和C4.5决策树，以及基于基尼增益的CART决策树。

    决策树算法采用自顶向下的递归方式，在决策树的内部结点进行属性值的比较，并根据不同的属性值判断从该结点向下的分支，在决策树的叶结点得到结论。

决策树算法的流程图：

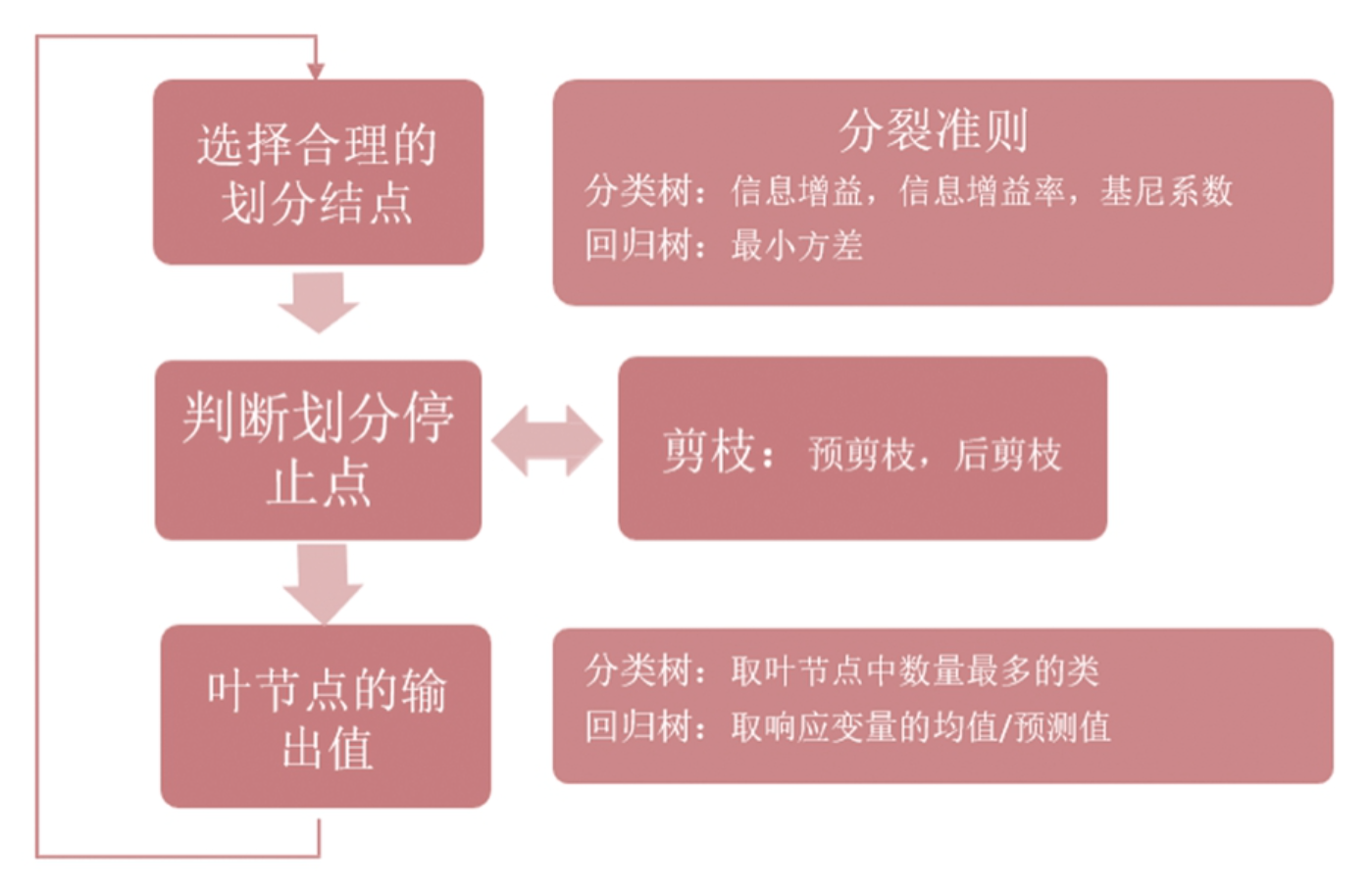
    从根结点到叶结点的一条路径对应着一条分类规则，整个决策树对应着一组分类规则。

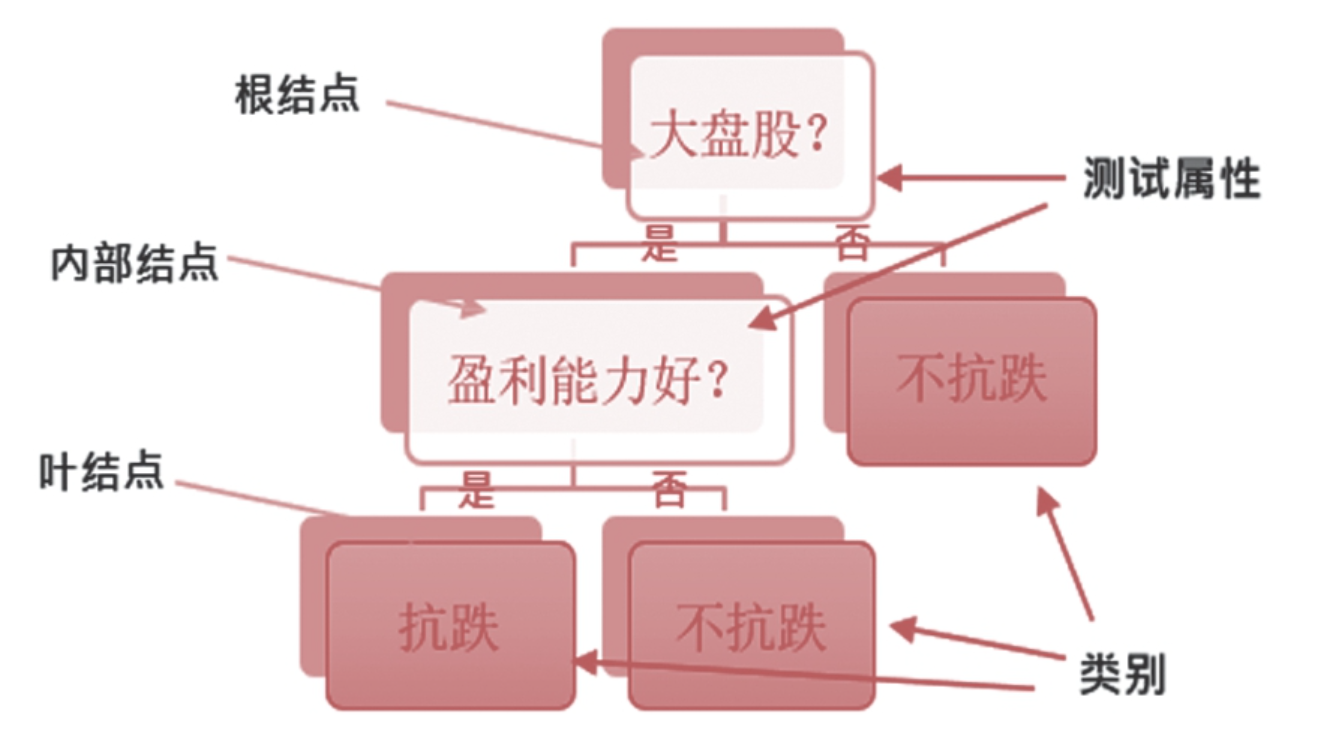
    使用决策树对某股票是否抗跌进行判断的展示效果，根结点表示的是对信息影响最大的属性（大盘股），如果不是大盘股，那么分支直接得到叶结点，其分类结果是不抗跌的；如果是大盘股，则判断其他属性，若盈利能力好，那么分类的结果是抗跌的，若盈利能力不好，那么叶结点的输出结果是不抗跌的。

2、决策树解读用户分群后的特征

    对于决策树结果，我们可以知道每个类别是根据哪个属性进行裂变划分的，这对我们解读聚类的结果有启发作用。

    对于决策树模型的搭建，我们可以直接使用sklearn中的框架，代码如下：