一、机器学习概述

一个目标：

给机器赋予人的智能，让机器能够像人一样地思考问题，做出决策

两种途径：

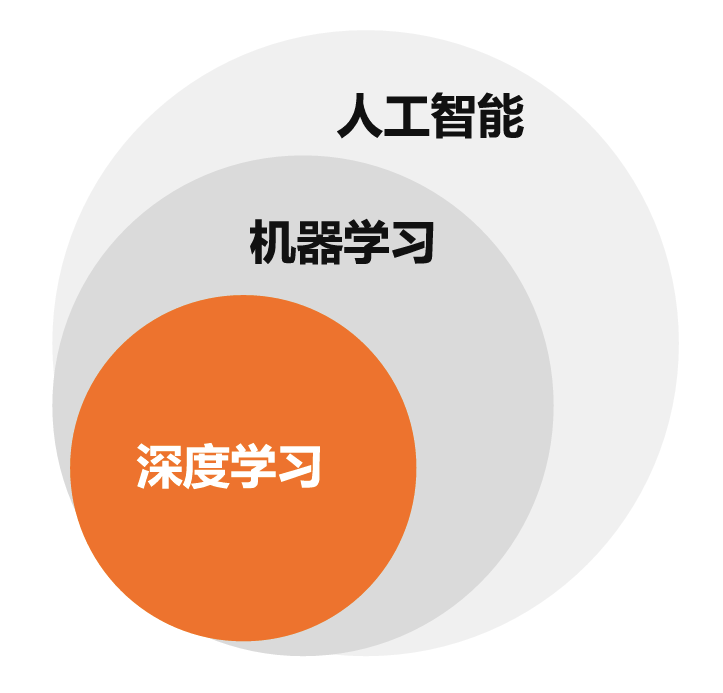
机器学习是实现人工智能的一种途径，让机器使用算法解析数据、从中学习数据特征，并进行归纳判断

深度学习是机器学习的一类重要方法，采用多层非线性函数（神经网络）学习数据特征，并进行判断，属于机器学习解决图像、语音、文本等领域问题的一个重要分支

机器学习的定义与方向：

通过技术的手段，利用已有的数据（经验）开发可以用来对新数据进行预测的模型；主要研究能产生模型的算法

基于学习方式的划分：根据学习的输入数据是否需要标注进行划分

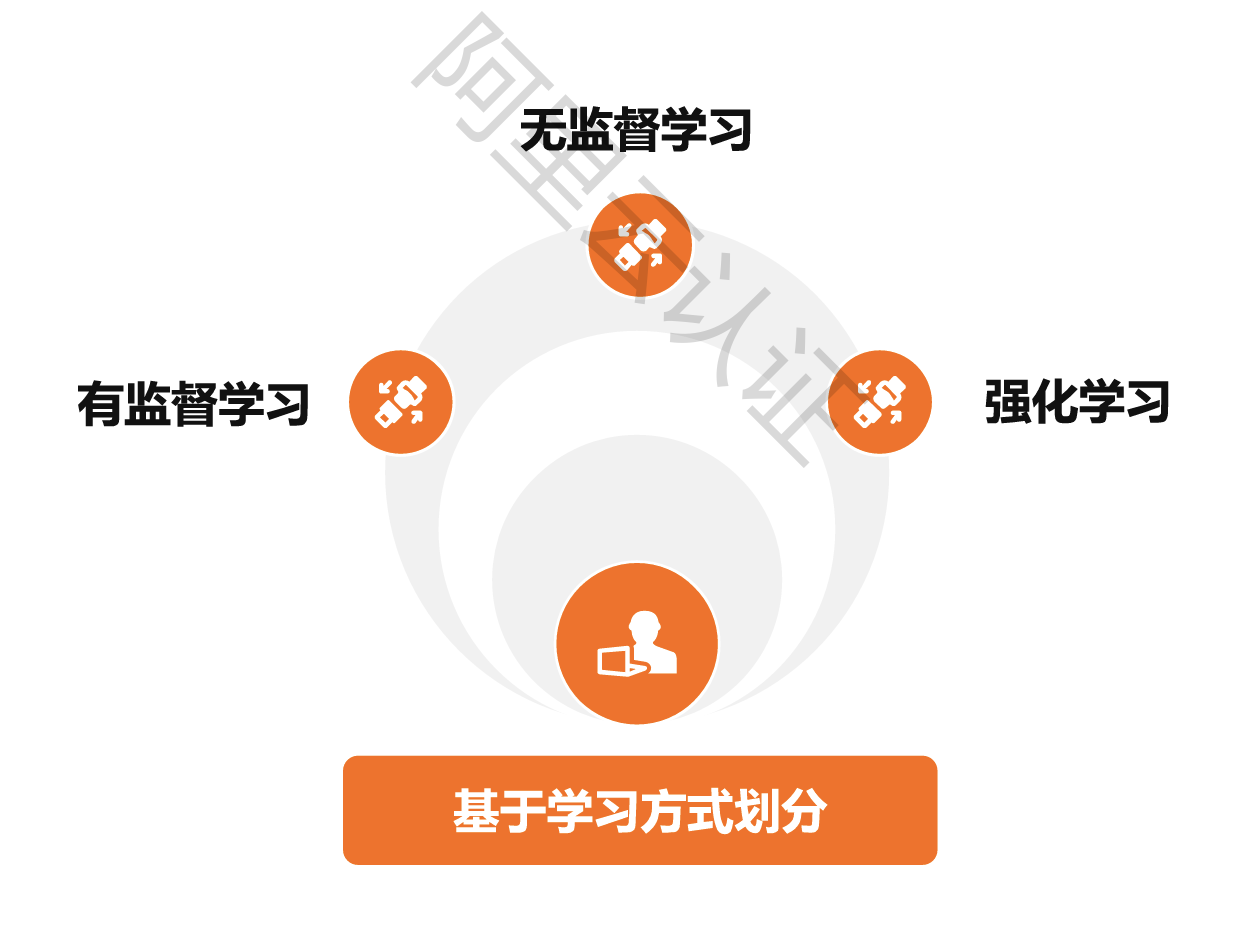
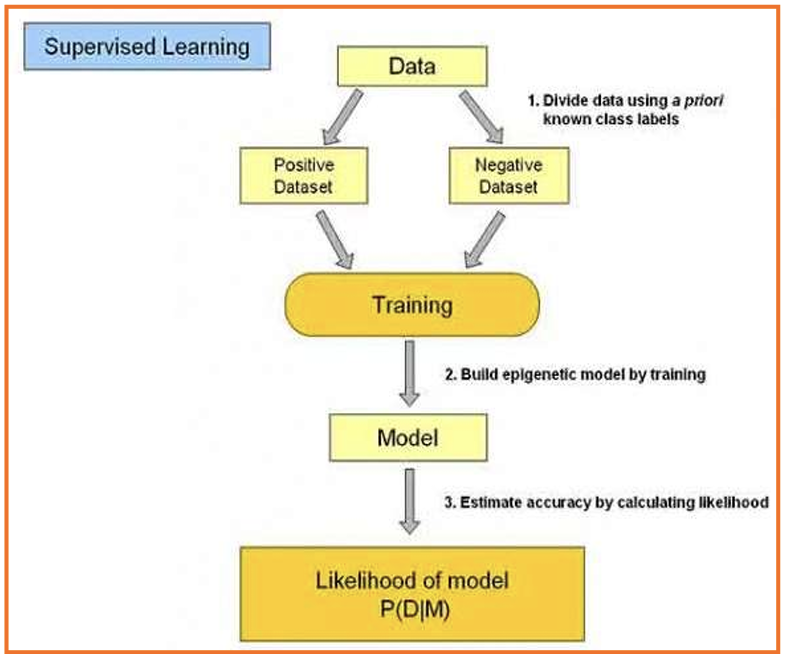
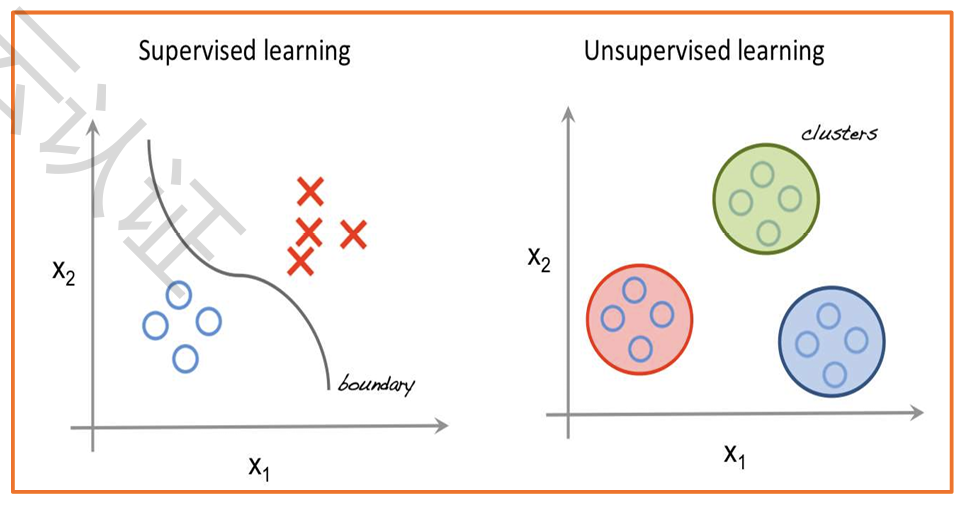
有监督学习：

输入数据：为“训练数据”，每组训练数据有明确标识

学习过程：将预测结果与“训练数据”的实际结果进行比较，不断调整预测模型，直到模型预测结果达到一个预期的准确率

应用场景：分类、回归

无监督学习：

输入数据：数据没有被明确标识

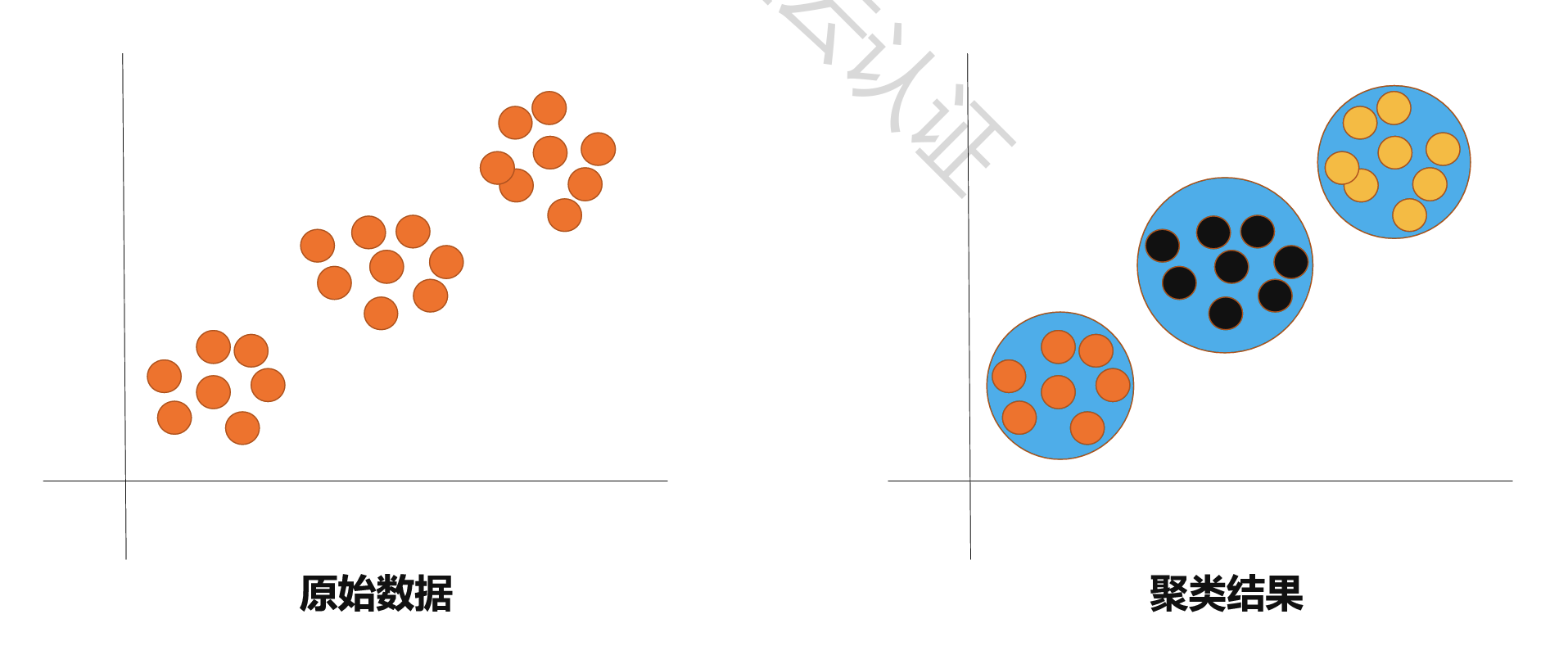
学习过程：不存在目标变量，基于数据本身去识别变量之间内在的模式和特征

应用场景：关联分析、聚类

强化学习：

一种机器学习方式：以“试错”的方式进行学习，通过与环境进行交互获得的奖赏指导行为，目标是使智能体获得最大的奖赏或实现特定目标

输入数据：不要求预先给定任何数据，通过接收环境对动作的奖励（反馈）获得学习信息

输出：模型参数调整

应用领域：机器人控制、计算机视觉、自然语言处理

基于学习策略的划分：根据学习策略是否基于经典数据原理还是模拟人脑感知进行划分

传统机器学习：

基于统计、概率、线性代数等数学原理，通过分析输入数据的模式，进行判断与预测

深度学习：

机器学习的一个重要分支

通过模拟人类大脑感知与组织的工作方式，通过人工神经网络构建，分析输入数据，进行判断与预测

分类与回归：

定义：分类就是将不同的类别进行分开。而回归则是找到一个空间，使得数据点尽可能的落在空间上

分类：预测变量是离散的；如 今天天气为晴天

回归：预测变量是连续的；如 今天气温为36.4度

区别：输出和目的进行区分

机器学习常见函数

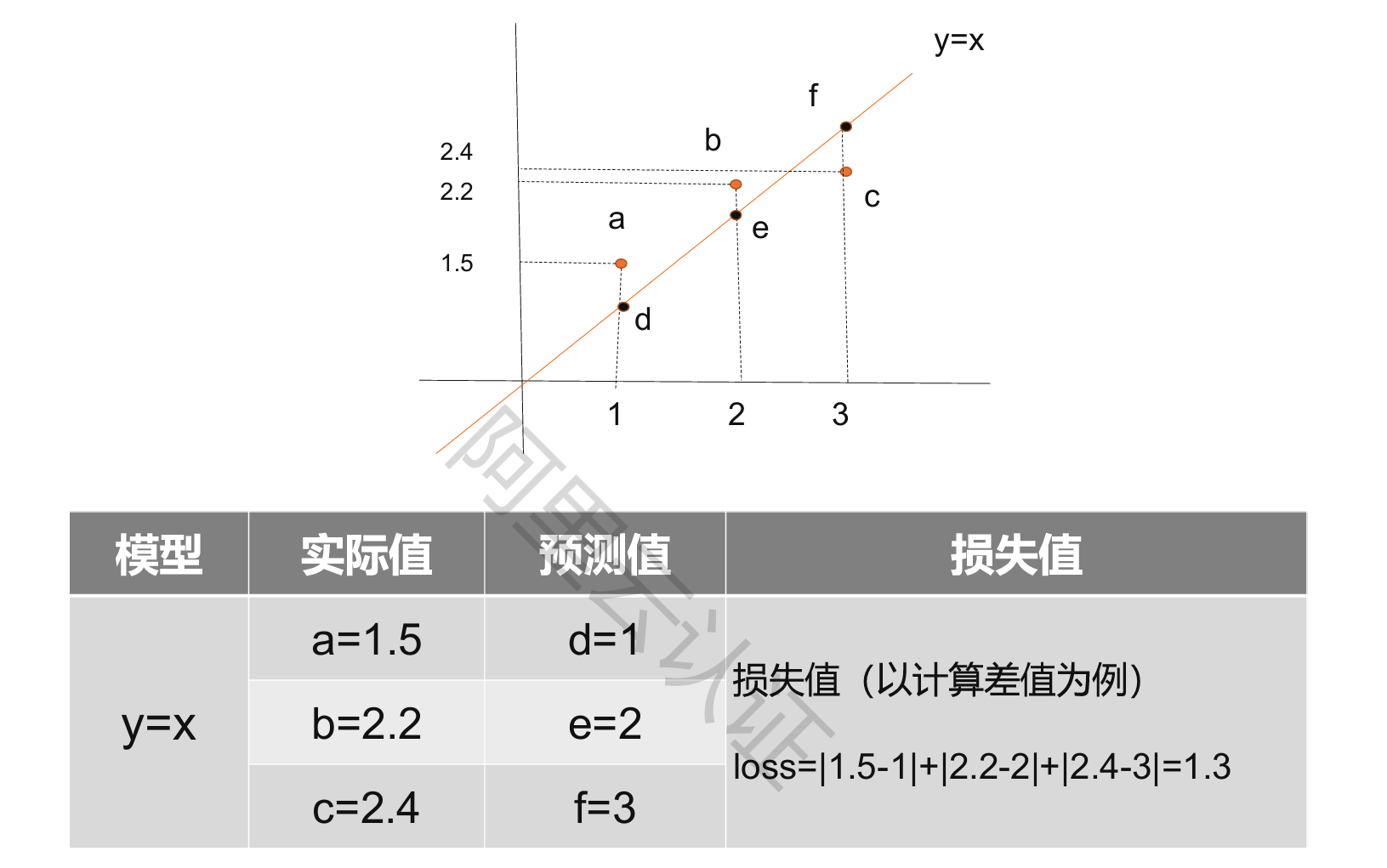
损失函数

用来估量模型的预测试与真实值的不一致程度，是一个非负实值函数

损失函数的值越小，说明模型的预测值与真实值越接近

不同的算法可能使用的损失函数不同

优化函数

通过调节参数使误差函数值变小

常见的优化函数：

批量梯度下降 BGD：易收敛，每次学习使用整个样本集，学习一次的时间长

小批量梯度下降法 MBGD：每次学习使用小批量样本集，结合了BGD的SGD的优点，弱化了缺点

随机梯度下降法 SGD：每次学习使用随机单个样本，学习一次时间短。下降会出现损失函数波动且难收敛

牛顿法

动量优化法

适用性梯度算法

均方根传播算法

AdaDelta算法

Adam算法

优化函数的执行过程：

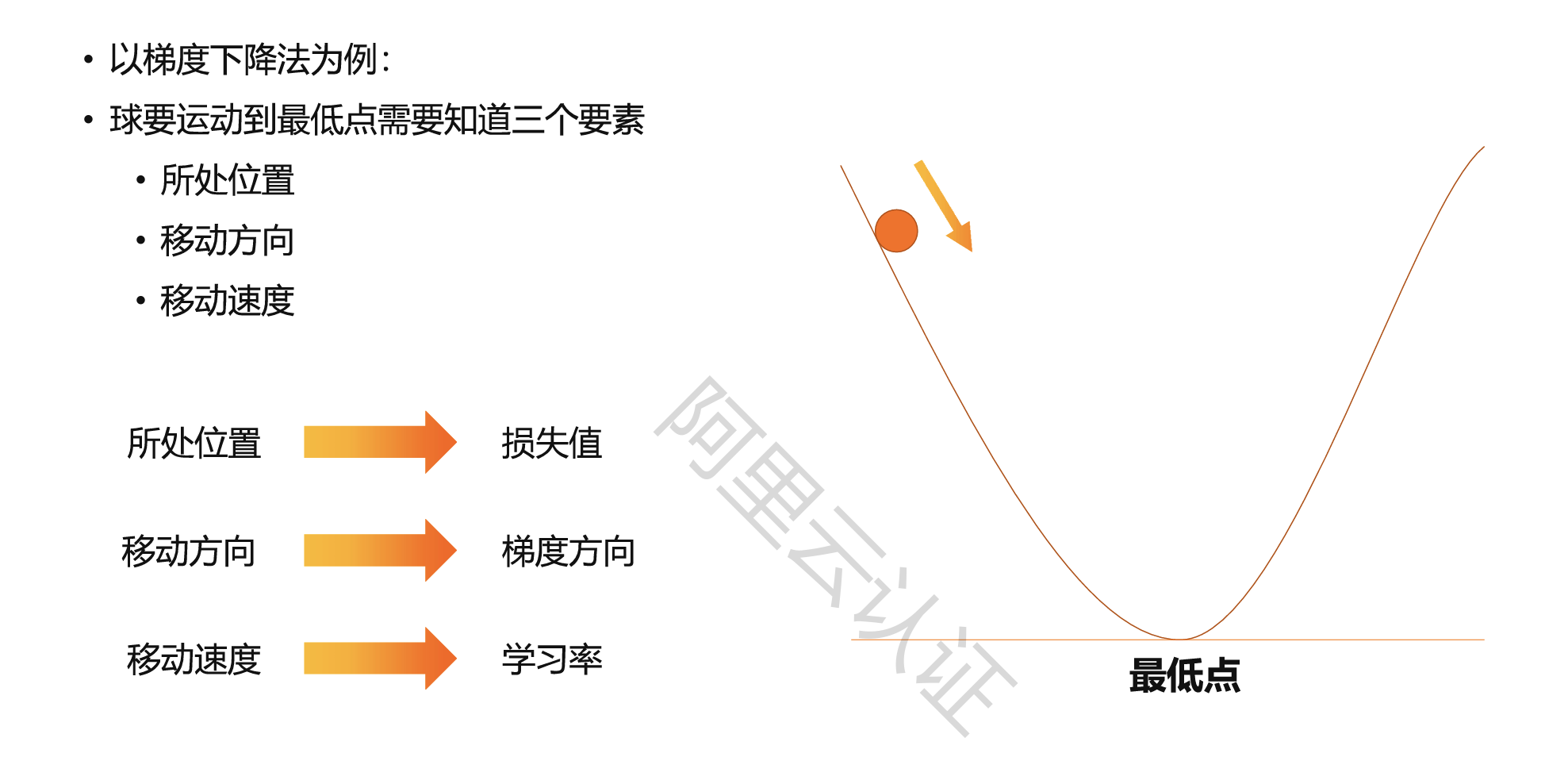
以梯度下降法为例：

球要运动到最低点需要直到三个要素：所处位置、移动方向、移动速度

机器学习常见评估指标：

评价指标建立在不同的机器学习任务上，主要分为三类：分类、回归、无监督

分类任务：

混淆矩阵

准确率

精确度和召回率

F1分数

回归任务：

均方误差MSE

平均绝对误差MAE

均方根误差RMSE

无监督任务：

兰德系数

互信息

轮廓系数

二、机器学习经典算法介绍

线性回归

利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法

任务类型：回归

场景：异常指标监控、贷款预测

欠拟合：模型在训练集、测试集上均表现不佳

过拟合：在训练集上表现很好，到了验证个测试阶段就很差

线性回归正则化模型

正则化能有效的防止过拟合现象

根据正则化 的选择，线性回归正则化模型有3种：

岭回归（线性回归L2正则化）

Lasso回归（线性回归L1正则化）

弹性网络回归（结合L1和L2正则化）：它在处理高维数据和具有多重共线性的特征时表现出色，可以有效地减少模型的过拟合，并在存在高度相关的特征时保持稳定性

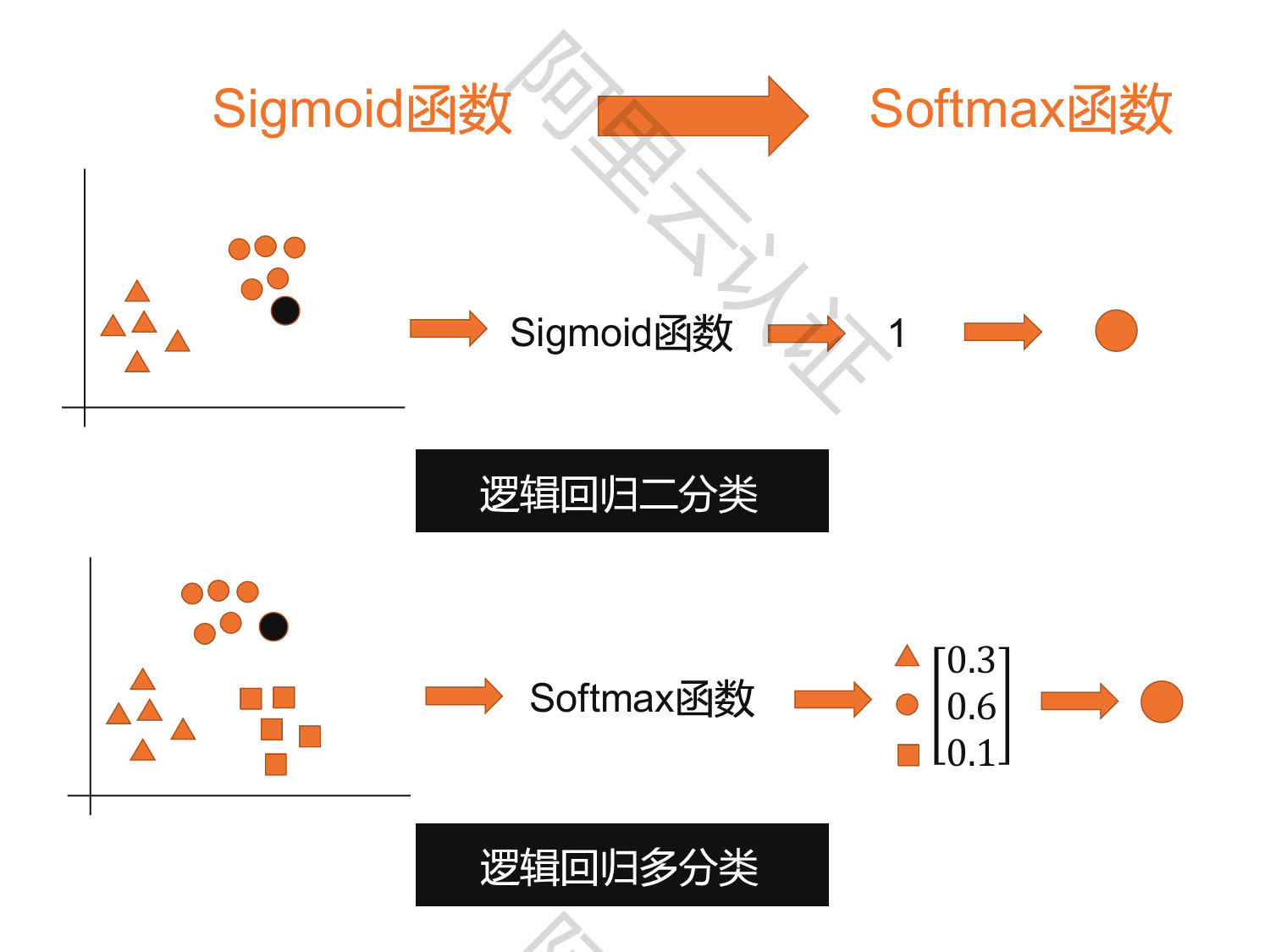
逻辑回归

广义线性回归，在线性回归的基础上添加非线性变换，使得逻辑回归输出值为离散型

任务类型：分类

应用场景：天气预测

逻辑回归多分类应用：

一对多法：

对L分类，训练时依次把某个类别的样本归为一类，其他剩余的样本归为一类，得到K个分类器

预测时分别用K个分类器进行预测，选择结果最大的作为分类的结果

优点：普适性比较广，效率较高

缺点：易造成数据不平衡

一对一法：

对K分类，训练时依次让不同类别数据两两组合训练，得到 k(k-1) / 2 个分类模型

预测时分别用二分类器进行预测，最后得票最多的类别即为未知样本的类别

优点：一定程度规避数据不平衡情况，性能相对稳定，训练效率提高

缺点：训练的二分类模型更多，影响预测时间

softmax法

朴素贝叶斯

基于贝叶斯定理与特征条件独立假设的分类方法

任务类型：分类

场景：垃圾邮件分类、舆情分析

什么是特征条件独立假设呢？

比如要根据温度、湿度、是否出太阳等3个特征判断今天是否会下雨。实际这3个特征是相互关联的，但是为了简化计算，朴素贝叶斯假设这3个特征相互独立

K近邻

从训练集中找到与新实例最近的K歌实例，根据K个实例来进行预测

任务类型：分类、回归

场景：约会匹配、商品推荐

距离度量：

欧氏距离

曼哈顿距离

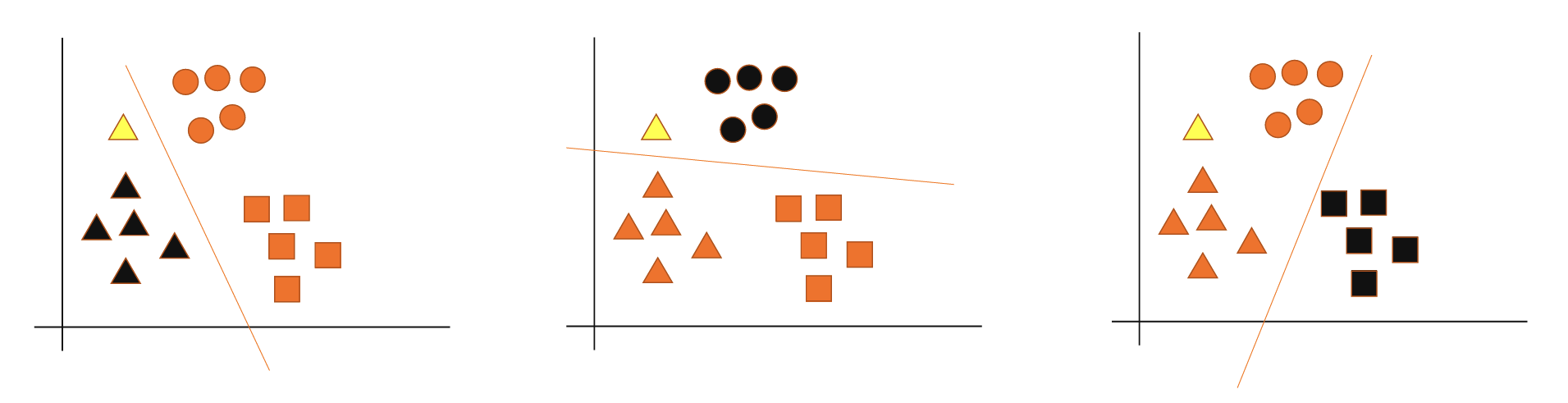
支持向量机

支持向量机是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面

场景：心脏病预测、用户窃电识别

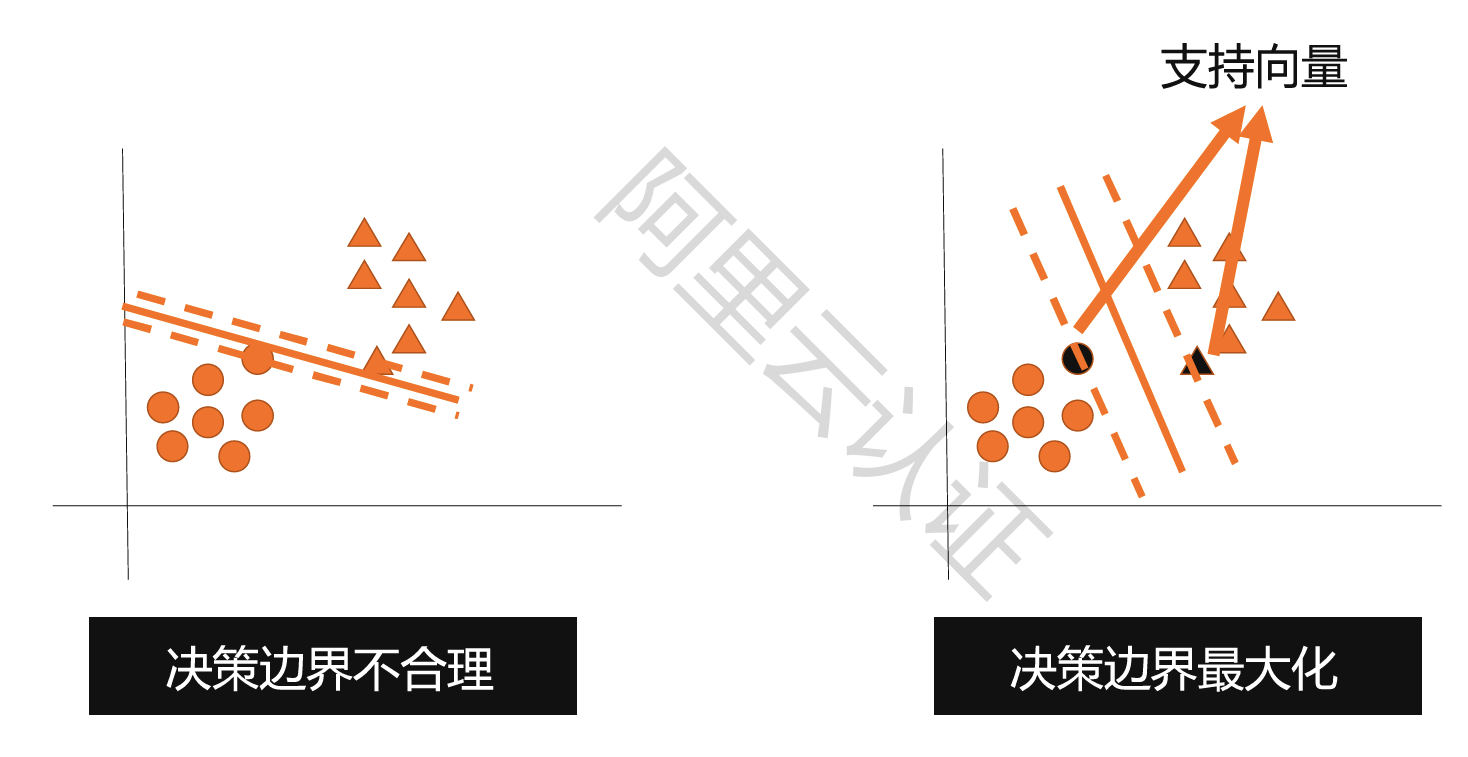
线性可分：如果样本可以直接使用一个线性函数切分，则称样本线性可分

线性不可分：如果样本不能直接使用一个线性函数切分，则称样本线性不可分。通过升维，将低维度映射到高维度实现线性可分

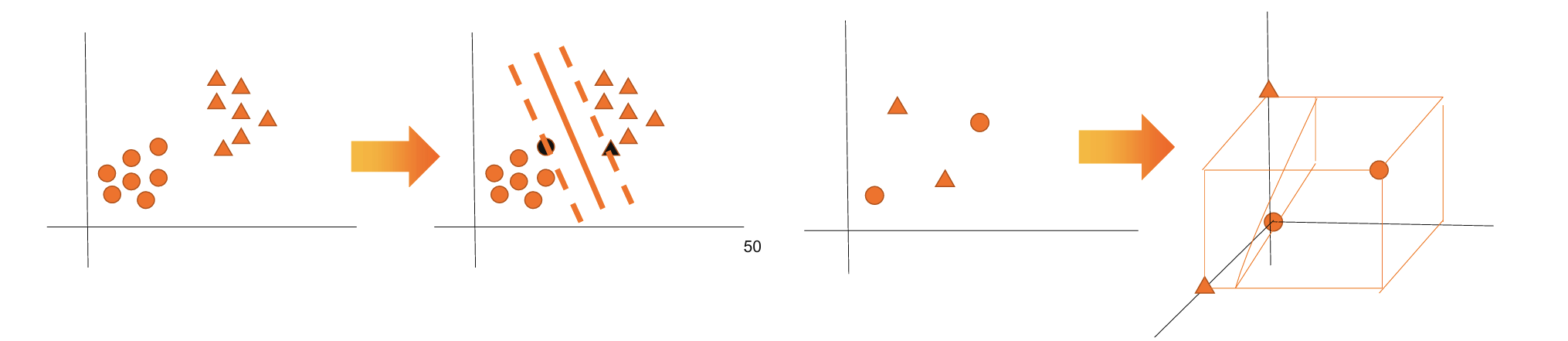
为了解决支持向量机线性不可分，引入核函数概念

核函数：将数据样本升维，使低维非线性可分变为高维线性可分

常见核函数：线性核函数、径向基核函数、多项式核函数、sigmoid核函数

决策树

一种以树结构形式来表达的预测分析模型

类别：分类树和回归树

场景：贷款预测、动物识别

决策树结构：由节点和分支构成

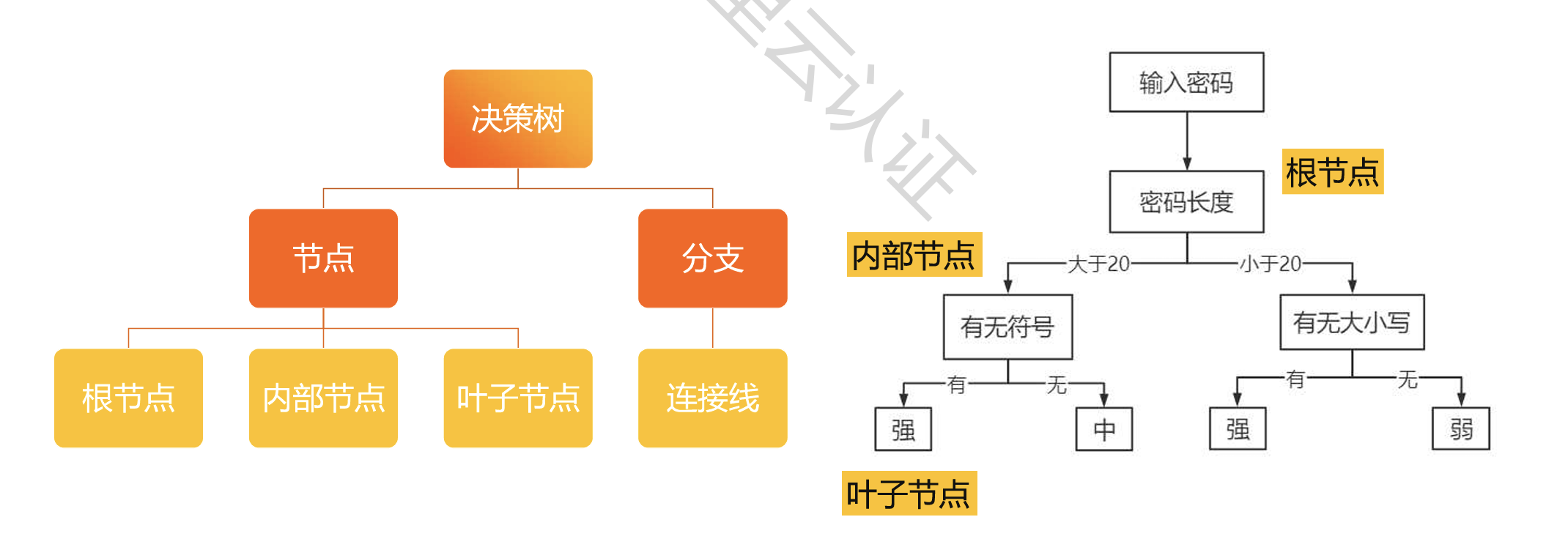
决策树构建步骤：

特征选择：信息熵、信息增益率、基尼系数

决策树生成：ID3算法（分类）、C4.5算法（分类）、CART算法（分类和回归）

决策树剪枝：预剪枝（边构造决策树边剪枝）、后剪枝（构造完决策树后剪枝）

集成算法

通过构建和结合多个机器学习算法（基学习器）完成学习任务

重要条件：基学习器学习结果之间存在差异

场景：土地覆盖测绘、恶意软件检测

集成学习算法的三大流派：、

Bagging：

主要对样本训练集合进行随机化抽样，通过反复的抽样训练新的模型，最终在这些模型的基础上取平均

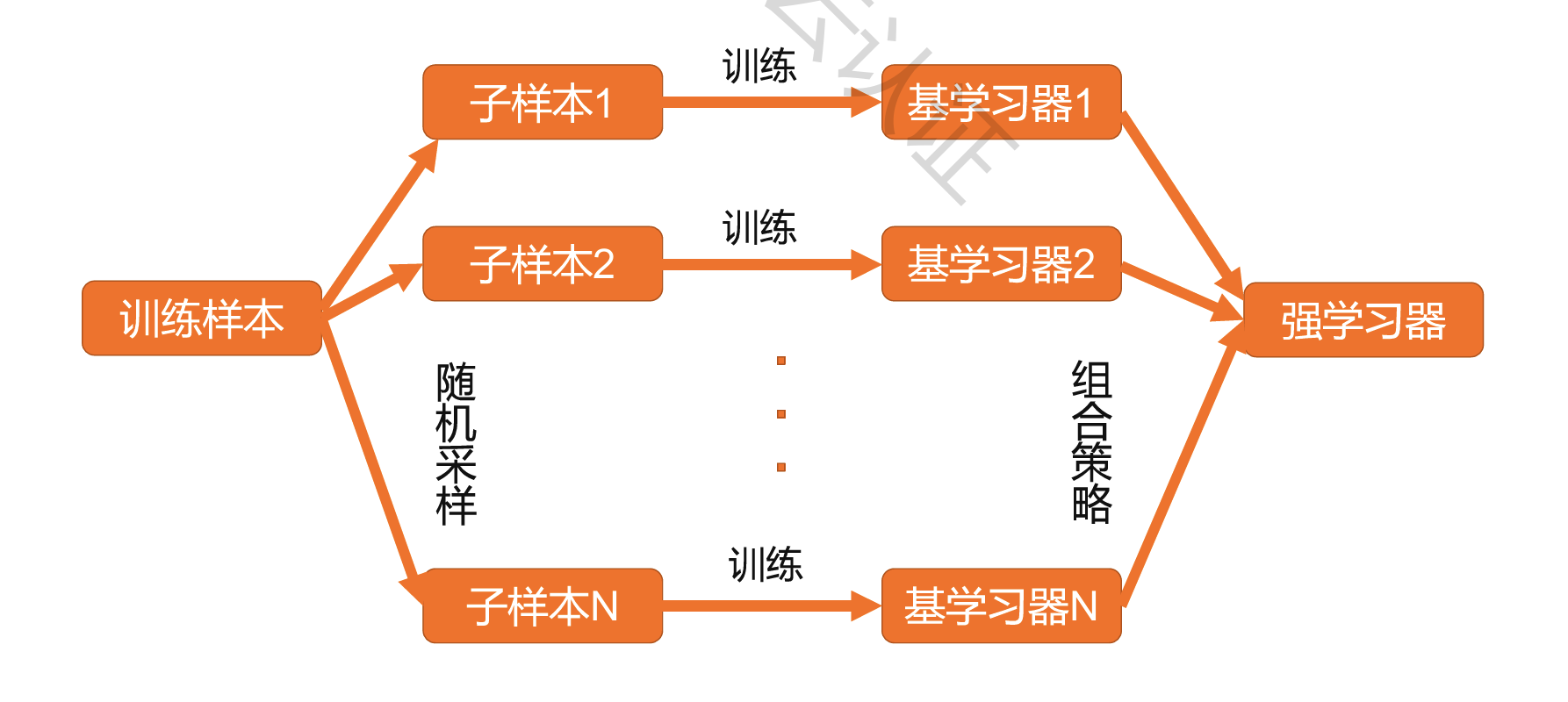
Boosting：

通过不断地使用一个弱学习器弥补前一个弱学习器的“不足”的过程，来串行地构造一个较强的学习器，这个强学习器能够使目标函数值足够小

Stacking：

通过一个元分类器或者元回归器来整合多个分类模型或回归模型的集成学习技术。基础模型利用整个训练集做训练，元模型将基础模型的输出作为特征进行训练

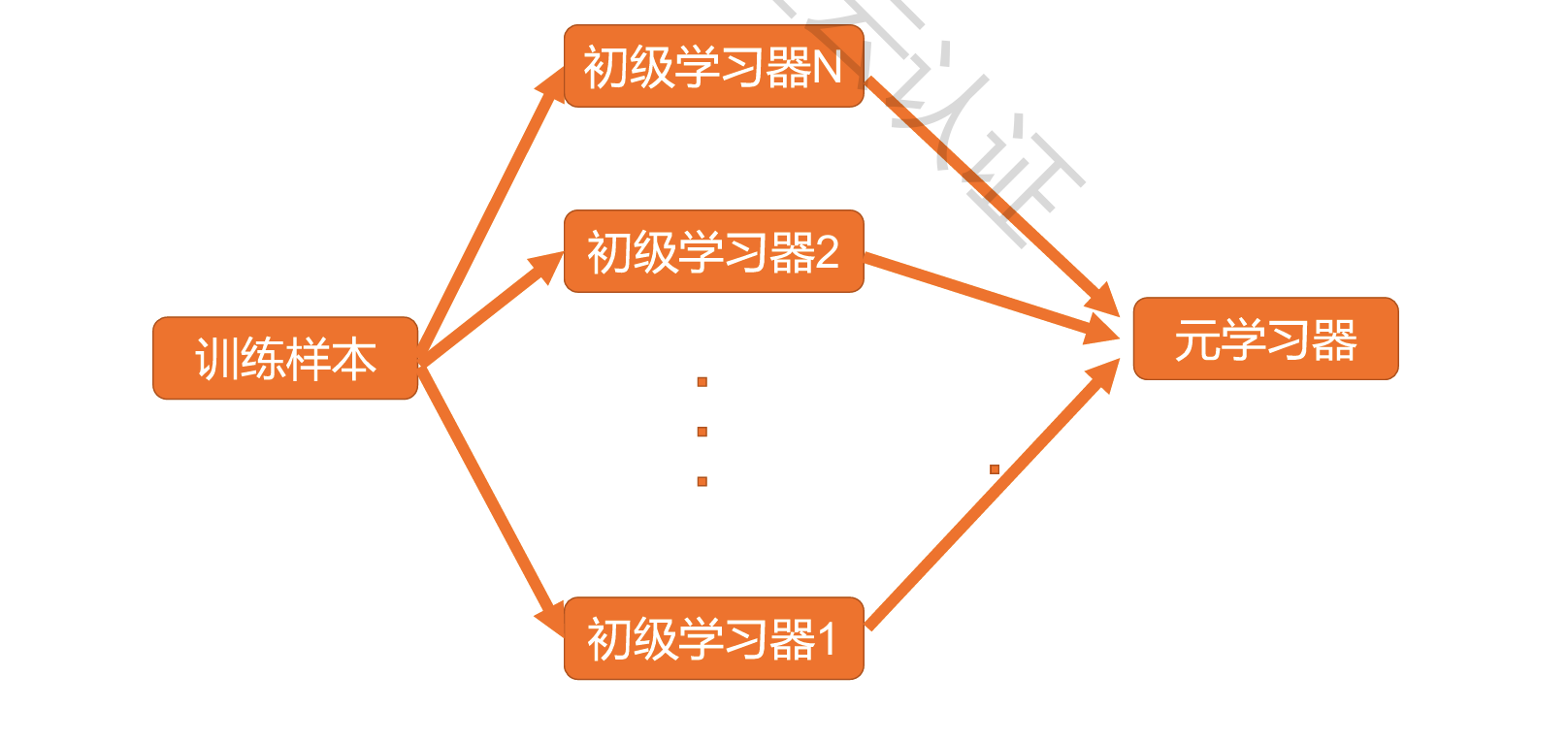
聚类算法

属于无监督学习的一种，使同一类的数据尽可能聚集到一起，不同数据尽量分离

场景：非人恶意流量识别、新闻主题聚类

三、机器学习PAI简单实现