一、函数本义溯源

    函数，函，为含，包含之意，还有匣、盒之意；数，这里指变化的数，函数就是包含变化数的数学式。是一种变化引起另外一种变化的数学工具，怎么引起变化呢？那就需要一种规则。所以函数就包含这三个要素：一种变化、另外一种变化、中间规则，也就是自变量、因变量、对应法则。

    函数，最早由中国清朝数学家李善兰翻译，出于其著作《代数学》。之所以这么翻译，他给出的原因是“凡此变数中函彼变数者，则此为彼之函数”，也即函数指一个量随着另一个量的变化而变化，或者说一个量中包含另一个量。

    函数（function），数学术语。其定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。函数的近代定义是给定一个数集A，假设其中的元素为x，对A中的元素x施加对应法则f，记作f（x），得到另一数集B，假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示，函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

二、什么叫做函数？

    函数，函，为含，包含之意，还有匣、盒之意；数，这里指变化的数，函数就是包含变化数的数学式。是一种变化引起另外一种变化的数学工具，怎么引起变化呢？那就需要一种规则。所以函数就包含这三个要素：一种变化、另外一种变化、中间规则，也就是自变量、因变量、对应法则。

传统的数学定义：在一个变化过程中，假设有两个变量x、y，如果对于任意一个x都有唯一确定的一个y和它对应。也就是说自变量x数量没有做限制，可以是一个或多个，但是因变量y数量就做了限制，只能是唯一，并且y的值是确定的。

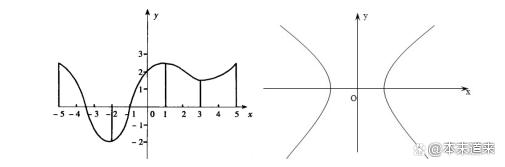
如果利用图形表示就是自变量x取值不同，但是应变量y可以是同一个确定的值，符合函数概念；但是一个自变量x，对应两个应变量y,不符合函数定义，故不是函数。

我们可以把函数理解为机器，自变量就是原料，因变量就是成品，原料通过特定的机器做特定的成品。

比如原料是白面粉，通过馒头机，只能做出白馒头；原料是黑面粉，通过馒头机，只能做出黑馒头。这里说明只要对应法则一定，因变量是随着自变量的变化而变化。

又比如原料是枣泥和面粉两种原料，通过馒头机，做出枣泥馒头一种产品，这说明自变量可以是两种或者多种，但因变量只能是一种确定的结果。为什么需要结果是唯一确定的呢？因为数学就是一门逻辑严密的学科，要求结果是确定的。

我们通常利用字母x表示成原料，字母y表示成品，它们具有泛指性，可以代替你想代表的一切，对应规则就是,我们可以写成,也可以写成，这里的，f是函数英文名字（function）头字母，表示成品、结果，（x）中的x就是原料、输入。

三、什么是复合函数？

复合函数就是嵌套函数，里层函数的结果为外层函数的输入量，就是变化引起一种变化，这种变化结果在引起另外一种变化。例如面粉通过馒头机做出馒头，把馒头当作原料通过馒头片机做出馒头片。就好像俄罗斯套娃。写成， 内部 ，外部就是；内层的结果是，作为外层输入。

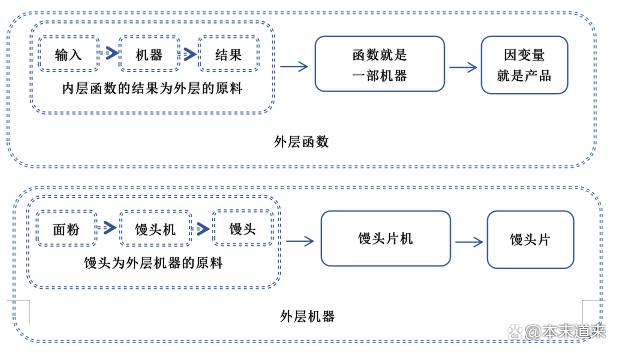
四、什么是反函数？

函数就是原料经过函数机器加工成为产品，反函数就是产品可以经过反函数机器还原成原料。

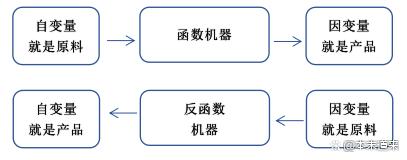
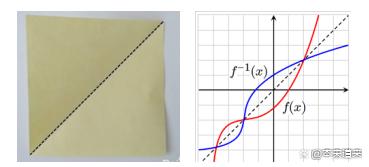
例如原函数是：，它的反函数就是,其实就把字母对调一下，但是我们习惯把y看作因变量，所示我们把反函数整理成：。对调字母深层含义就是X轴和Y轴对调，也就是沿着轴做镜像，联想一张直角的纸，沿着对角线对折，对角线就是轴。这就是反函与原函数关于轴对原因。

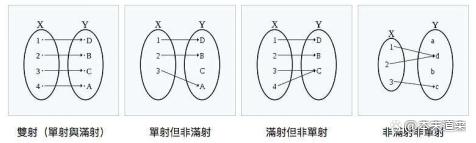
如果要是原函数具有反函数，根据函数定义，自变量对应唯一确定的因变量，反函数也是函数复合函数定义，就是因变量对应唯一确定的自变量。要想原函数具有反函数，那就要确定唯一的自变量对应确定唯一的应变量，所以要求原函数单调，只有单调才可以一一对应。

五、为什么研究函数的单调性呢？

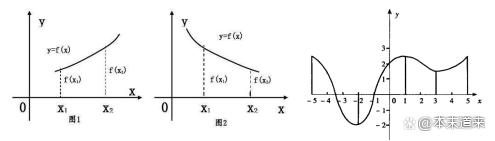
单调性，顾名思义，就是朝一个方向发展，或者随着自变量变大而变大，或者自变量的变大而减小。研究函数的单调性就是在自变量变化的时候，预判结果是朝哪个方向发展。如果函数整体不具有单调性，那么我们也会把它分段，在每小段研究单调性，预判这段的结

果的发展方向。

六、为什么研究函数的奇偶性呢？

奇偶性也就是函数的对称性，研究对称性，可以减少研究的范围，只研究函数的一半就可以了。

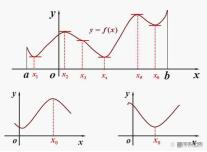
奇函数定义满足 。关于原点对称的函数，叫作奇函数。也就是自变量增加负号，结果也增加负号，自变量改变方向，因变量也改变方向。例如下图奇函数就是研究一半，绕着原点旋转180°就是另外一半，两部分本质上是相同的。

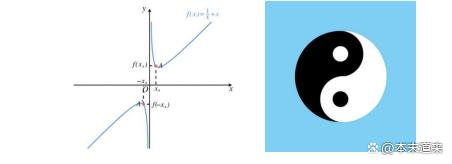
偶函数定义满足 。关于y轴对称的函数，叫作偶函数。也就是自变量增加负号，结果不改变，自变量改变方向，因变量还是原来方向。例如下图偶函数就是研究一半，绕着y轴做镜像，就是另外一半。

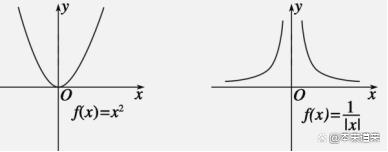
七、为什么研究函数的连续性呢？

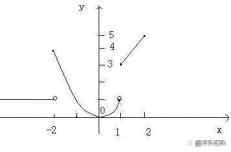
直观上来说，连续的函数就是当输入值的变化足够小的时候，输出的变化也会随之足够小的函数。如果输入值的某种微小的变化会产生输出值的一个突然的跳跃甚至无法定义，则这个函数被称为是不连续的函数；连续函数我们可以做无限切割，这是微积分的基础。不连续函数我们可以做分段处理，划分成部分连续函数，在做无限切割。

八、为什么研究函数的凹凸性呢？

函数凹凸性就是寻找函数的拐弯处，找到函数的拐弯处只知道函数在那个点方向开始变化，未来发展趋势有了改变；找到高点和低点。现实生活中我们往往是寻找最大点或者低点，比如汽车在什么路段开到那个速度省油，就是需要某段的最低点。